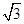题目内容
设函数 (其中
(其中 ).
).
(1) 当 时,求函数
时,求函数 的单调区间和极值;
的单调区间和极值;
(2) 当 时,函数
时,函数 在
在 上有且只有一个零点.
上有且只有一个零点.
 (其中
(其中 ).
).(1) 当
 时,求函数
时,求函数 的单调区间和极值;
的单调区间和极值;(2) 当
 时,函数
时,函数 在
在 上有且只有一个零点.
上有且只有一个零点.(1)函数 的递减区间为
的递减区间为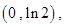 递增区间为
递增区间为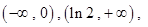 极大值为
极大值为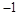 ,极小值为
,极小值为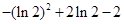 ;(2)详见试题解析.
;(2)详见试题解析.
 的递减区间为
的递减区间为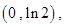 递增区间为
递增区间为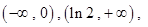 极大值为
极大值为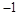 ,极小值为
,极小值为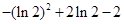 ;(2)详见试题解析.
;(2)详见试题解析.试题分析:(1)先求
 ,解方程
,解方程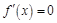 ,得
,得 可能的极值点,列表可得函数
可能的极值点,列表可得函数 的单调区间和极值;(2)
的单调区间和极值;(2) .当
.当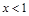 时,
时,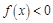 ,
,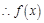 在
在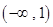 上无零点,故只需证明函数
上无零点,故只需证明函数 在
在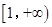 上有且只有一个零点.分
上有且只有一个零点.分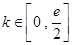 和
和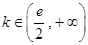 利用函数的单调性证明函数
利用函数的单调性证明函数 在
在 上有且只有一个零点.
上有且只有一个零点.试题解析:(1)当
 时,
时,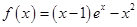 ,
,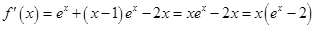 .
.令
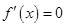 ,得
,得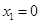 ,
,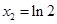 .
.当
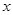 变化时,
变化时,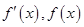 的变化如下表:
的变化如下表: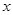 | 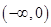 |  | 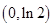 | 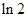 | 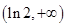 |
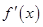 | 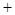 |  | 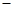 |  | 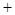 |
 |  | 极大值 |  | 极小值 |  |
 的递减区间为
的递减区间为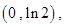 递增区间为
递增区间为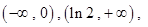 极大值为
极大值为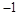 ,极小值为
,极小值为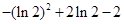 . 6分
. 6分(2)
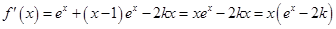 .当
.当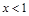 时,
时,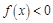 ,
,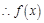 在
在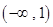 上无零点,故只需证明函数
上无零点,故只需证明函数 在
在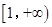 上有且只有一个零点.
上有且只有一个零点.①若
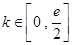 ,则当
,则当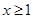 时,
时,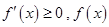 在
在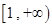 上单调递增.
上单调递增.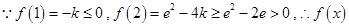 在上
在上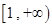 有且只有一个零点.
有且只有一个零点.②若
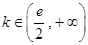 ,则
,则 在
在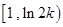 上单减,
上单减,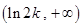 上单增.
上单增. 令
令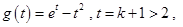 则
则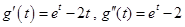 .
. 在
在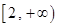 上单增,
上单增,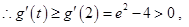
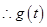 在
在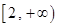 上单增,
上单增,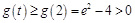 ,
,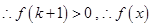 在
在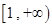 上有且只有一个零点.
上有且只有一个零点.综上,
 在
在 上有且只有一个零点. 13分
上有且只有一个零点. 13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 在
在 处的切线垂直
处的切线垂直 轴,求
轴,求 的值;
的值; 上为增函数,求
上为增函数,求 的单调性.
的单调性. ,(其中m为常数).
,(其中m为常数).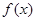 在区间
在区间 上的单调性;
上的单调性; .当
.当 时,曲线
时,曲线 上总存在相异两点
上总存在相异两点 、
、 ,使得过
,使得过 、
、 点处的切线互相平行,求
点处的切线互相平行,求 的取值范围.
的取值范围.
 ,求
,求 的单调区间,
的单调区间, 时,
时, ,求
,求 的取值范围.
的取值范围. -
-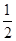 alnx,a∈R.
alnx,a∈R.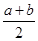 )≤
)≤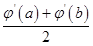 ≤φ′(
≤φ′(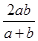 ).
).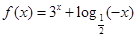 的零点所在区间为( )
的零点所在区间为( )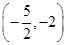
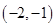

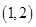
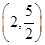
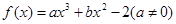 有且仅有两个不同的零点
有且仅有两个不同的零点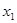 ,
,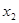 ,则( )
,则( ) 时,
时, ,
,
 ,
,
 时,
时,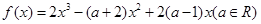 .
.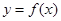 在
在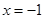 处的切线方程为
处的切线方程为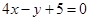 ,求实数
,求实数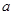 的值.
的值.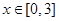 时,不等式
时,不等式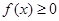 恒成立,求实数
恒成立,求实数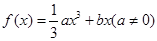 ,若f(3)="3f" ′(x0),则x0=( )
,若f(3)="3f" ′(x0),则x0=( )