题目内容

已知向量
m
=(2cosωx，1)，
n
=(
3
sinωx-cosωx，a)，其中（x∈R，ω＞0），函数f(x)=
m
•
n
的最小正周期为π，最大值为3．
（I）求ω和常数a的值；
（Ⅱ）求函数f（x）的单调递增区间．
（I）f(x)=
m
•
n
=2
3
sinωxcosωx-2cos2ωx+a（1分）
=
3
sin2ωx-cos2ωx-1+a=2sin(2ωx-
π
6
)+a-1（3分）
由T=
2π
2ω
=π，得ω=1．（4分）
又当sin(2ωx-
π
6
)=1时ymax=2+a-1=3，得a=2（6分）
（Ⅱ）由（I）知f(x)=2sin(2x-
π
6
)+1当2kπ-
π
2
≤2x-
π
6
≤2kπ+
π
2
(k∈Z)（8分）
即kπ-
π
6
≤x≤kπ+
π
3
（10分）
故f（x）的单调增区间为[kπ-
π
6
，kπ+
π
3
]，（k∈Z）（12分）
练习册系列答案
相关题目
已知向量
m
=(2cosωx，1)，
n
=(
3
sinωx-cosωx，a)，其中（x∈R，ω＞0），函数f(x)=
m
•
n
的最小正周期为π，最大值为3．
（I）求ω和常数a的值；
（Ⅱ）求函数f（x）的单调递增区间．
已知向量
 m 
=(2cosα ， 2sinα)，
 n 
=(3cosβ ， 3sinβ)，若
 m 
与
 n 
的夹角为60°，则直线 xcosα-ysinα+
1
2
=0与圆(x-cosβ)2+(y+sinβ)2=
1
2
的位置关系是（　　）
A、相交但不过圆心B、相交过圆心
C、相切D、相离
已知向量m=(2cosα，2sinα)，n=(2sinβ，2cosβ)，|m+n|=
8
5
5
．
（Ⅰ）求sin（α+β）的值；
（Ⅱ）设0＜α＜
π
2
，-
π
2
＜β＜0，cosβ=
12
13
，求cosα的值．
（2009•河西区二模）已知向量
m
=(2cosωx，1)，
n
=(
3
sinωx-cosωx，a)，函数f(x)=
m
•
n
，（x∈R，ω＞0）的最小正周期为
π
2
，最大值为3．
（I）求ω和常数a的值；
（Ⅱ）求函数f（x）的单调增区间及使f（x）≥0成立的x的取值集合．
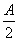在△ABC中，角A，B，C的对边分别为 a，b，c．已知向量m=(2cos，sin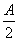)，n=(cos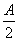，-2sin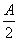)，m·n=-1，
(1)求cosA的值；
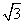(2)若a=2，b=2，求c的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网