题目内容
已知向量m=(2cosα,2sinα),n=(2sinβ,2cosβ),|m+n|=8
| ||
| 5 |
(Ⅰ)求sin(α+β)的值;
(Ⅱ)设0<α<
| π |
| 2 |
| π |
| 2 |
| 12 |
| 13 |
分析:(1)通过向量的加法运算和模的运算可得到sin(α+β)的值.
(2)由α=(α+β)-β,运用两角差的余弦定理可得答案.
(2)由α=(α+β)-β,运用两角差的余弦定理可得答案.
解答:(Ⅰ)解:∵m+n=(2cosα+2sinβ,2sinα+2cosβ),
∴|m+n|=2
=2
.
∴2
=
.
∴sin(α+β)=
;
(Ⅱ)解:∵0<α<
,-
<β<0,
∴-
<α+β<
.
又∵sin(α+β)=
,∴sinβ=-
,cos(α+β)=
∵α=(α+β)-β,
∴cosα=cos(α+β)cosβ+sin(α+β)sinβ=
×
-
×
=
.
∴|m+n|=2
| (cosα+sinβ)2+(sinα+cosβ)2 |
| 2+2sin(α+β) |
∴2
| 2+2sin(α+β) |
8
| ||
| 5 |
∴sin(α+β)=
| 3 |
| 5 |
(Ⅱ)解:∵0<α<
| π |
| 2 |
| π |
| 2 |
∴-
| π |
| 2 |
| π |
| 2 |
又∵sin(α+β)=
| 3 |
| 5 |
| 5 |
| 13 |
| 4 |
| 5 |
∵α=(α+β)-β,
∴cosα=cos(α+β)cosβ+sin(α+β)sinβ=
| 4 |
| 5 |
| 12 |
| 13 |
| 3 |
| 5 |
| 5 |
| 13 |
| 33 |
| 65 |
点评:本题主要考查向量的坐标运算和三角函数中的两角差的余弦公式.向量和三角的综合是高考中必考题,尤其是向量的坐标运算和两角和与差的正余弦公式的结合更是高考的热点.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
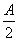 ,sin
,sin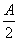 ),n=(cos
),n=(cos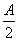 ,-2sin
,-2sin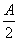 ),m·n=-1,
),m·n=-1,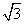 ,b=2,求c的值.
,b=2,求c的值.