题目内容
在平面直角坐标系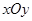 中,已知圆心在
中,已知圆心在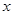 轴上、半径为
轴上、半径为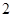 的圆
的圆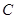 位于
位于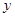 轴右侧,且与直线
轴右侧,且与直线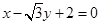 相切.
相切.
(1)求圆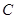 的方程;
的方程;
(2)在圆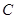 上,是否存在点
上,是否存在点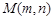 ,使得直线
,使得直线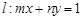 与圆
与圆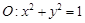 相交于不同的两点
相交于不同的两点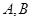 ,且
,且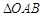 的面积最大?若存在,求出点
的面积最大?若存在,求出点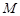 的坐标及对应的
的坐标及对应的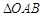 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
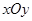 中,已知圆心在
中,已知圆心在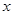 轴上、半径为
轴上、半径为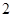 的圆
的圆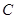 位于
位于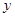 轴右侧,且与直线
轴右侧,且与直线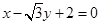 相切.
相切. (1)求圆
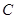 的方程;
的方程;(2)在圆
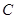 上,是否存在点
上,是否存在点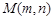 ,使得直线
,使得直线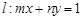 与圆
与圆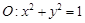 相交于不同的两点
相交于不同的两点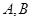 ,且
,且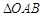 的面积最大?若存在,求出点
的面积最大?若存在,求出点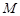 的坐标及对应的
的坐标及对应的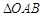 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.(1) ;
;
(2) 时取得最大值
时取得最大值 ,点
,点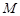 的坐标是
的坐标是 与
与 ,面积的最大值是
,面积的最大值是 .
.
 ;
;(2)
 时取得最大值
时取得最大值 ,点
,点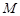 的坐标是
的坐标是 与
与 ,面积的最大值是
,面积的最大值是 .
. 试题分析:(1)设圆心是
 ,它到直线
,它到直线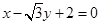 的距离是
的距离是 ,
,解得
 或
或 (舍去) 4分
(舍去) 4分 所求圆
所求圆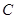 的方程是
的方程是 6分
6分(2)
 点
点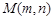 在圆
在圆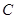 上
上
 ,
, 且
且
又
 原点到直线
原点到直线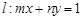 的距离
的距离 8分
8分解得
 9分
9分而


 11分
11分 12分
12分 当
当 ,即
,即 时取得最大值
时取得最大值 ,
,此时点
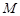 的坐标是
的坐标是 与
与 ,面积的最大值是
,面积的最大值是 . 14分
. 14分点评:中档题,求圆的方程,一般利用待定系数法,本题解法是从确定圆心、半径入手,体现解题的灵活性。直线与圆的位置关系问题,往往涉及圆的“特征三角形”,利用勾股定理解决弦长计算问题。

练习册系列答案
相关题目
 经过点
经过点 ,则( )
,则( )



 ,过点
,过点 的直线
的直线 与圆相交于
与圆相交于 两点,
两点, ,则直线
,则直线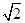 ,则实数m的取值范围是( ).
,则实数m的取值范围是( ).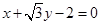 被圆
被圆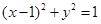 截得的线段的长为( )
截得的线段的长为( )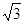
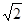
 和圆
和圆 相交于点
相交于点 。
。 的垂直平分线方程;(2)求弦
的垂直平分线方程;(2)求弦 R
R 与圆
与圆 的交点个数是( )
的交点个数是( ) ,设该圆中过点
,设该圆中过点 的最长弦和最短弦分别为
的最长弦和最短弦分别为 和
和 ,则四边形
,则四边形 的面积是 ___________
的面积是 ___________ 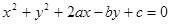 表示圆心为C(2,2),半径为2的圆,则
表示圆心为C(2,2),半径为2的圆,则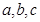 的值依次为 ( )
的值依次为 ( ) 、4、4;
、4、4;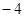 、4;
、4;