题目内容
已知△ABC的三个内角A、B、C成等差数列,且AB=1,BC=4,则边BC上的中线AD的长为 .
【答案】分析:先根据三个内角A、B、C成等差数列和三角形内角和为π可求得B的值,进而利用AD为边BC上的中线求得BD,最后在△ABD中利用余弦定理求得AD.
解答:解:∵△ABC的三个内角A、B、C成等差数列
∴A+C=2B
∵A+B+C=π
∴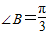
∵AD为边BC上的中线
∴BD=2,
由余弦定理定理可得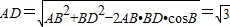
故答案为: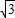
点评:本题主要考查等差中项和余弦定理,涉及三角形的内角和定理,难度一般.
解答:解:∵△ABC的三个内角A、B、C成等差数列
∴A+C=2B
∵A+B+C=π
∴
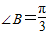
∵AD为边BC上的中线
∴BD=2,
由余弦定理定理可得
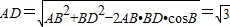
故答案为:
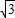
点评:本题主要考查等差中项和余弦定理,涉及三角形的内角和定理,难度一般.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目