题目内容
如图,点P是椭圆 +
+ =1上一动点,点H是点M在x轴上的射影,坐标平面xOy内动点M满足:
=1上一动点,点H是点M在x轴上的射影,坐标平面xOy内动点M满足: (O为坐标原点),设动点M的轨迹为曲线C.
(O为坐标原点),设动点M的轨迹为曲线C.(Ⅰ)求曲线C的方程;
(Ⅱ)过右焦点F的直线l交曲线C于D,E两点,且2
 =
= ,点E关于x轴的对称点为G,求直线GD的方程.
,点E关于x轴的对称点为G,求直线GD的方程.
【答案】分析:(Ⅰ)设动点M(x,y),P(x,y),则H(x,0),由动点M满足: (O为坐标原点),得出坐标之间的关系,利用P(x,y)是椭圆
(O为坐标原点),得出坐标之间的关系,利用P(x,y)是椭圆 +
+ =1上一动点,即可求出曲线C的方程;
=1上一动点,即可求出曲线C的方程;
(Ⅱ)直线l:y=k(x-1),设D(x1,y1),E(x2,y2),由于2 =
= ,得坐标之间的关系,联立
,得坐标之间的关系,联立 ,得(1+k2)x2-2k2x+k2-4=0,利用韦达定理,即可求得k=
,得(1+k2)x2-2k2x+k2-4=0,利用韦达定理,即可求得k= ,
, ,
, ,再分
,再分 ,
, 分别求得求直线GD的方程.
分别求得求直线GD的方程.
解答: 解:(Ⅰ)设动点M(x,y),P(x,y),则H(x,0),
解:(Ⅰ)设动点M(x,y),P(x,y),则H(x,0),
由动点M满足: (O为坐标原点),即
(O为坐标原点),即
∴
∵P(x,y)是椭圆 +
+ =1上一动点
=1上一动点
∴
∴
∴x2+y2=4
∴曲线C的方程为x2+y2=4
(Ⅱ)直线l:y=k(x-1),设D(x1,y1),E(x2,y2),由于2 =
= ,
,
则
∴x2=3-2x1
联立 ,得(1+k2)x2-2k2x+k2-4=0,
,得(1+k2)x2-2k2x+k2-4=0,
则 x1+x2= ,…①x1x2=
,…①x1x2= ,…②,
,…②,
x2=3-2x1代入①、②得, ,…③
,…③ ,…④
,…④
由③、④得k= ,
, …(9分)
…(9分)
∴ ,
,
(i)若 时,
时, ,
, ,
,
∴ ,
,
∴ ,
,
∴直线GD的方程是 ,即
,即 ;
;
(ii)当 时,同理可求直线GD的方程是
时,同理可求直线GD的方程是 …(12分)
…(12分)
点评:本题重点考查轨迹方程,考查直线与圆的位置关系,考查向量知识的运用,解题时联立方程,利用韦达定理是关键
 (O为坐标原点),得出坐标之间的关系,利用P(x,y)是椭圆
(O为坐标原点),得出坐标之间的关系,利用P(x,y)是椭圆 +
+ =1上一动点,即可求出曲线C的方程;
=1上一动点,即可求出曲线C的方程;(Ⅱ)直线l:y=k(x-1),设D(x1,y1),E(x2,y2),由于2
 =
= ,得坐标之间的关系,联立
,得坐标之间的关系,联立 ,得(1+k2)x2-2k2x+k2-4=0,利用韦达定理,即可求得k=
,得(1+k2)x2-2k2x+k2-4=0,利用韦达定理,即可求得k= ,
, ,
, ,再分
,再分 ,
, 分别求得求直线GD的方程.
分别求得求直线GD的方程.解答:
 解:(Ⅰ)设动点M(x,y),P(x,y),则H(x,0),
解:(Ⅰ)设动点M(x,y),P(x,y),则H(x,0),由动点M满足:
 (O为坐标原点),即
(O为坐标原点),即
∴

∵P(x,y)是椭圆
 +
+ =1上一动点
=1上一动点∴

∴

∴x2+y2=4
∴曲线C的方程为x2+y2=4
(Ⅱ)直线l:y=k(x-1),设D(x1,y1),E(x2,y2),由于2
 =
= ,
,则

∴x2=3-2x1
联立
 ,得(1+k2)x2-2k2x+k2-4=0,
,得(1+k2)x2-2k2x+k2-4=0,则 x1+x2=
 ,…①x1x2=
,…①x1x2= ,…②,
,…②,x2=3-2x1代入①、②得,
 ,…③
,…③ ,…④
,…④由③、④得k=
 ,
, …(9分)
…(9分)∴
 ,
,(i)若
 时,
时, ,
, ,
,∴
 ,
,
∴
 ,
,∴直线GD的方程是
 ,即
,即 ;
;(ii)当
 时,同理可求直线GD的方程是
时,同理可求直线GD的方程是 …(12分)
…(12分)点评:本题重点考查轨迹方程,考查直线与圆的位置关系,考查向量知识的运用,解题时联立方程,利用韦达定理是关键

练习册系列答案
相关题目
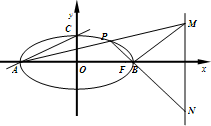 如图,设点P是椭圆
如图,设点P是椭圆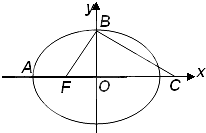 (2009•泰安一模)如图,点F是椭圆
(2009•泰安一模)如图,点F是椭圆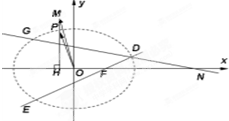 (2011•西山区模拟)如图,点P是椭圆
(2011•西山区模拟)如图,点P是椭圆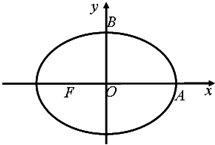 如图,点F是椭圆W:
如图,点F是椭圆W: