题目内容
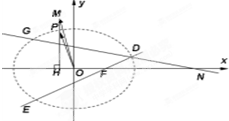 (2011•西山区模拟)如图,点P是椭圆
(2011•西山区模拟)如图,点P是椭圆| x2 |
| 4 |
| y2 |
| 3 |
| 3 |
| HM |
| HP |
(Ⅰ)求曲线C的方程;
(Ⅱ)过右焦点F的直线l交曲线C于D,E两点,且2
| DF |
| FE |
分析:(Ⅰ)设动点M(x,y),P(x0,y0),则H(x,0),由动点M满足:
=2
(O为坐标原点),得出坐标之间的关系,利用P(x0,y0)是椭圆
+
=1上一动点,即可求出曲线C的方程;
(Ⅱ)直线l:y=k(x-1),设D(x1,y1),E(x2,y2),由于2
=
,得坐标之间的关系,联立
,得(1+k2)x2-2k2x+k2-4=0,利用韦达定理,即可求得k=±
,x1=
,x2=3-2x1=-
,再分k=
,k=-
分别求得求直线GD的方程.
| 3 |
| HM |
| HP |
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)直线l:y=k(x-1),设D(x1,y1),E(x2,y2),由于2
| DF |
| FE |
|
| ||
| 3 |
| 7 |
| 4 |
| 1 |
| 2 |
| ||
| 3 |
| ||
| 3 |
解答: 解:(Ⅰ)设动点M(x,y),P(x0,y0),则H(x,0),
解:(Ⅰ)设动点M(x,y),P(x0,y0),则H(x,0),
由动点M满足:
=2
(O为坐标原点),即
(0,y)=2(x0-x,y0)
∴
∵P(x0,y0)是椭圆
+
=1上一动点
∴
+
=1
∴
+
=1
∴x2+y2=4
∴曲线C的方程为x2+y2=4
(Ⅱ)直线l:y=k(x-1),设D(x1,y1),E(x2,y2),由于2
=
,
则
∴x2=3-2x1
联立
,得(1+k2)x2-2k2x+k2-4=0,
则 x1+x2=
,…①x1x2=
,…②,
x2=3-2x1代入①、②得,3-x1=
,…③3x1-2
=
,…④
由③、④得k=±
,x1=
…(9分)
∴x2=3-2x1=-
,
(i)若k=
时,y1=
(
-1)=
,y2=
(-
-1)=-
,
∴G(-
,
),D(
,
)
∴kGD=
=-
,
∴直线GD的方程是y-
=-
(x+
),即15x+9
y-60=0;
(ii)当k=-
时,同理可求直线GD的方程是15x-9
y-60=0…(12分)
 解:(Ⅰ)设动点M(x,y),P(x0,y0),则H(x,0),
解:(Ⅰ)设动点M(x,y),P(x0,y0),则H(x,0),由动点M满足:
| 3 |
| HM |
| HP |
| 3 |
∴
|
∵P(x0,y0)是椭圆
| x2 |
| 4 |
| y2 |
| 3 |
∴
| ||
| 4 |
| ||
| 3 |
∴
| x2 |
| 4 |
(
| ||||
| 3 |
∴x2+y2=4
∴曲线C的方程为x2+y2=4
(Ⅱ)直线l:y=k(x-1),设D(x1,y1),E(x2,y2),由于2
| DF |
| FE |
则
|
∴x2=3-2x1
联立
|
则 x1+x2=
| 2k2 |
| 1+k2 |
| k2-4 |
| 1+k2 |
x2=3-2x1代入①、②得,3-x1=
| 2k2 |
| 1+k2 |
| x | 2 1 |
| k2-4 |
| 1+k2 |
由③、④得k=±
| ||
| 3 |
| 7 |
| 4 |
∴x2=3-2x1=-
| 1 |
| 2 |
(i)若k=
| ||
| 3 |
| ||
| 3 |
| 7 |
| 4 |
| ||
| 4 |
| ||
| 3 |
| 1 |
| 2 |
| ||
| 2 |
∴G(-
| 1 |
| 2 |
| ||
| 2 |
| 7 |
| 4 |
| ||
| 4 |
∴kGD=
| ||||||||
|
| ||
| 9 |
∴直线GD的方程是y-
| ||
| 2 |
| ||
| 9 |
| 1 |
| 2 |
| 15 |
(ii)当k=-
| ||
| 3 |
| 15 |
点评:本题重点考查轨迹方程,考查直线与圆的位置关系,考查向量知识的运用,解题时联立方程,利用韦达定理是关键

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
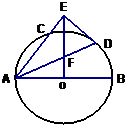 (2011•西山区模拟)如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.
(2011•西山区模拟)如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.