题目内容
(本小题满分12分)
已知等差数列{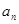 }的前n项和为Sn,且
}的前n项和为Sn,且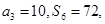
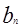 =
=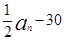
(1)求通项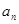 ;
;
(2)求数列{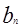 }的前n项和的最小值。
}的前n项和的最小值。
已知等差数列{
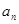 }的前n项和为Sn,且
}的前n项和为Sn,且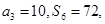
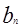 =
=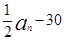
(1)求通项
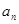 ;
; (2)求数列{
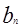 }的前n项和的最小值。
}的前n项和的最小值。(1) =4n-2(2)-225.
=4n-2(2)-225.
 =4n-2(2)-225.
=4n-2(2)-225.试题分析:(1)由
 =10,
=10, =72,得
=72,得
∴
 =4n-2,----------4
=4n-2,----------4(2)则bn =

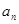 -30=2n-31.
-30=2n-31.
得
 ≤n≤
≤n≤ -------------------10 .
-------------------10 .∵n∈N*,∴n=15.
∴{
 }前15项为负值,∴
}前15项为负值,∴ 最小,---------------12
最小,---------------12可知
 =-29,d=2,∴
=-29,d=2,∴ =-225.----------------------12
=-225.----------------------12点评:等差数列的通项公式可化为
 ,是关于
,是关于 的一次函数,当
的一次函数,当 时为减函数且
时为减函数且 有最大值,取得最大值时的项数
有最大值,取得最大值时的项数 可由
可由 来确定;当
来确定;当 时为增函数且
时为增函数且 有最小值,取得最小值时的项数
有最小值,取得最小值时的项数 可由
可由 来确定.关键是要确定
来确定.关键是要确定 符号的转折点.
符号的转折点.
练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
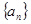 中,
中,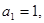 且点
且点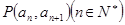 在直线
在直线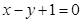 上。
上。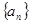 的通项公式;
的通项公式; (2)
(2)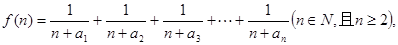 求函数
求函数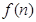 的最小值;
的最小值;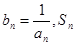 表示数列
表示数列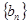 的前
的前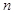 项和。试问:是否存在关于
项和。试问:是否存在关于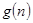 ,使得
,使得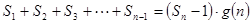 对于一切不小于2的自然数
对于一切不小于2的自然数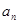 }的前n项和为
}的前n项和为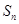 ,且
,且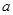 =1,
=1,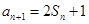 ,数列{
,数列{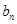 }满足
}满足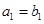 ,点P(
,点P(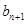 )在直线x―y+2=0上,
)在直线x―y+2=0上,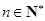 .
.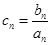 ,求数列{
,求数列{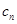 }的前n项和
}的前n项和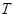 .
.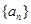 中,若
中,若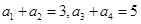 ,则
,则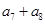 的和等于 ( )
的和等于 ( ) 的前
的前 项和
项和 ,则
,则 =
= 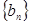 满足:
满足: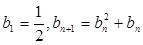 。
。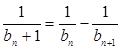 ;
;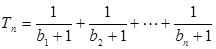 ,对任意的正整数
,对任意的正整数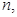
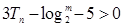 恒成立,求
恒成立,求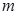 的取值范围。
的取值范围。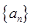 的前n项和为
的前n项和为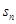 ,满足
,满足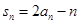
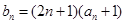 ,求数列
,求数列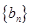 的前n项和
的前n项和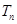 。
。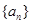 是公比为q的等比数列,其前n项的积为
是公比为q的等比数列,其前n项的积为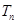 ,并且满足条件
,并且满足条件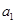 >1,
>1,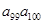 >1,
>1, 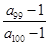 <0,给出下列结论:① 0<q<1;② T198<1;③
<0,给出下列结论:① 0<q<1;② T198<1;③