题目内容
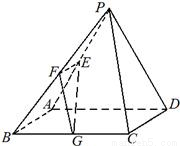
已知一个四棱锥P-ABCD的三视图(主视图与左视图为直角三角形,俯视图是带有一条对角线的正方形)如下,E是侧棱PC的中点。
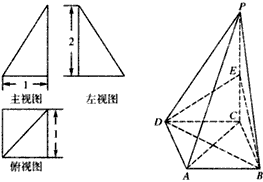
(1)求四棱锥P-ABCD的体积;
(2)求证:平面APC⊥平面BDE。
(2)求证:平面APC⊥平面BDE。
解:(1)由三视图可知,AB=BC=1,PC⊥面ABCD,且PC=2,
又底面ABCD是正方形,故S正方形ABCD=1,
所以 。
。
(2)证明:因为底面ABCD是正方形,
所以对角线AC⊥BD
又PC⊥面ABCD,而BD 面ABCD,
面ABCD,
故BD⊥PC,
又PC∩AC=C,
所以,BD⊥平面APC
又BD 平面BDE,
平面BDE,
故平面APC⊥平面BDE。
又底面ABCD是正方形,故S正方形ABCD=1,
所以
 。
。(2)证明:因为底面ABCD是正方形,
所以对角线AC⊥BD
又PC⊥面ABCD,而BD
 面ABCD,
面ABCD, 故BD⊥PC,
又PC∩AC=C,
所以,BD⊥平面APC
又BD
 平面BDE,
平面BDE, 故平面APC⊥平面BDE。

练习册系列答案
相关题目
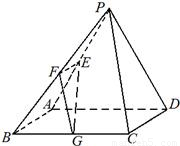
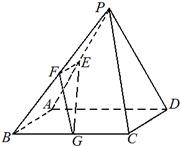 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PA、PB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PA、PB、BC的中点. B.
B. C.
C.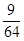 D.
D.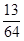
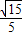 ?
?
 ?
?