题目内容
【题目】2018年高考特别强调了要增加对数学文化的考查，为此某校高三年级特命制了一套与数学文化有关的专题训练卷（文、理科试卷满分均为100分），并对整个高三年级的学生进行了测试，现从这些学生中随机抽取了50名学生的成绩，按照成绩为
，
，…，
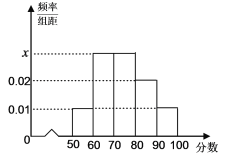
分成了5组，制成了如图所示的频率分布直方图（假定每名学生的成绩均不低于50分）.
（Ⅰ）求频率分布直方图中的
的值，并估计所抽取的50名学生成绩的中位数（用分数表示）；
（Ⅱ）若利用分层抽样的方法从样本中成绩不低于70分的三组学生中抽取6人，再从这6人中随机抽取2人参加这次考试的考后分析会，试求
组中至少有1人被抽到的概率.
【答案】（1）
（2）
【解析】分析：（Ⅰ）先计算第2、3组的频率和，再根据概率求x的值，再利用中位数公式求所抽取的50名学生成绩的中位数.( Ⅱ)利用古典概型求
组中至少有1人被抽到的概率.
详解：（Ⅰ）由频率分布直方图可得第2、3组的频率和为
， 故
.
设中位数为
分，则有
，
，
即所求的中位数为
分.
（Ⅱ）由（Ⅰ）可知，后三组中的人数分别为15,10,5，故这三组中所抽取的人数分别为3,2,1.
记成绩在
这组的3名学生分别为
，
，
，成绩在
这组的2名学生分别为
，
，成绩在
这组的1名学生为
，则从中任抽取3人的所有可能结果为
、
、
、
、
、
、
、
、
、
、
、
、
、
、
.共15种.
其中组中至少有1人被抽到的所有可能结果为、、、、、、、、、、、.共12种
故组中至少有1人被抽到的概率
.
练习册系列答案
相关题目
