题目内容
已知函数 ,且
,且
(1)当 ,求函数
,求函数 的极值;
的极值;
(2)设
①当 时,对任意
时,对任意 ,都有
,都有 成立,求
成立,求 的最大值;
的最大值;
②设 为
为 的导函数,若存在
的导函数,若存在 ,使得
,使得 成立,求
成立,求 的取值范围。
的取值范围。
解:(1)当 ,
, 时,
时, ,定义域为(-∞,0)∪(0,+∞).
,定义域为(-∞,0)∪(0,+∞).
所以 .
.
令 ,得
,得 ,列表
,列表
|
|
|
|
|
|
|
|
|
|
|
| - | - |
|
|
|
| ↗ | 极大值 | ↘ | ↘ | 极小值 | ↗ |
由表知 的极大值是
的极大值是 ,
, 的极小值是
的极小值是 . ……4分
. ……4分
(2)① 因为 ,
,
当 时,
时, .
.
因为 在
在 上恒成立,
上恒成立,
所以 在
在 上恒成立.
上恒成立.
记 ,则
,则 .
.
当 时,
时, ,
, 在
在 上是减函数;
上是减函数;
当 时,
时, ,
, 在
在 上是增函数.
上是增函数.
所以 .
.
所以 的最大值为
的最大值为 .
.
②因为 ,所以
,所以 .
.
由
 ,得
,得 ,
,
整理得 .
.
存在x>1,使g (x)+g ′(x)=0成立等价于存在x>1,使2ax3-3ax2-2bx+b=0 成立.
因为 ,所以
,所以 .
.
设 ,则
,则 .
.
因为 时,
时, 恒成立,所以
恒成立,所以 在
在 是增函数,
是增函数,
所以 ,
,
所以 ,即
,即 的取值范围为
的取值范围为 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目










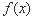 =
=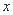 |
|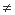 0,方程
0,方程 满足约束条件
满足约束条件 ,且目标函数
,且目标函数 的最大值是
的最大值是  图象上关于坐标原点
图象上关于坐标原点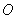 对称的点有
对称的点有 对,则
对,则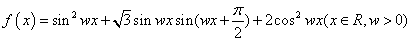 ,在
,在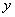 轴右侧的第一个最高点的横坐标
轴右侧的第一个最高点的横坐标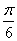 ,若将函数
,若将函数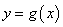 的图象。
的图象。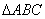 中,
中,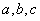 分别是角
分别是角 的对边,
的对边,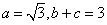 且
且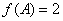 ,
, 若
若 在
在 上单调递增,则实数
上单调递增,则实数 的取值范围为( )
的取值范围为( ) B.
B. C.
C. D.
D.
 ,在
,在 轴上的截距是
轴上的截距是 轴上的截距的2倍,则直线方程为_____________________
轴上的截距的2倍,则直线方程为_____________________ ,函数
,函数 与函数
与函数 的图象可能是( )
的图象可能是( )



 上的动点
上的动点 到直线
到直线 的最小距离为(
的最小距离为( )
) B
B C.
C. D.
D.