题目内容
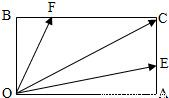
 如图,在矩形OACB中,E和F分别是边AC和BC的点,满足AC=3AE,BC=3BF,若
如图,在矩形OACB中,E和F分别是边AC和BC的点,满足AC=3AE,BC=3BF,若| OC |
| OE |
| OF |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
分析:在矩形OACB中,
=
+
,再化简
=λ
+μ
,比较系数可得
=1,
=1,可求λ+μ 的值.
| OC |
| OA |
| OB |
| OC |
| OE |
| OF |
| 3λ+μ |
| 3 |
| 3μ+λ |
| 3 |
解答:解:在矩形OACB中,
=
+
,
,
=λ
+μ
=λ(
+
)+μ(
+
)=λ(
+
)+μ(
+
)=
+
,
∴
=1,
=1,
=2,
∴λ+μ=
,
故选 B.
| OC |
| OA |
| OB |
,
| OC |
| OE |
| OF |
| OA |
| AE |
| OB |
| BF |
| OA |
| 1 |
| 3 |
| OB |
| OB |
| 1 |
| 3 |
| OA |
| 3λ+μ |
| 3 |
| OA |
| 3μ+λ |
| 3 |
| OB |
∴
| 3λ+μ |
| 3 |
| 3μ+λ |
| 3 |
| 4μ+4λ |
| 3 |
∴λ+μ=
| 3 |
| 2 |
故选 B.
点评:本题考查向量的运算法则、平面向量的基本定理及其意义,充分利用相等的向量.

练习册系列答案
相关题目
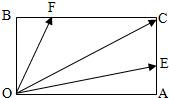
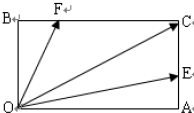 如图,在矩形OACB中,E和F分别是边AC和BC上的点,满足AC=3AE,BC=3BF,若
如图,在矩形OACB中,E和F分别是边AC和BC上的点,满足AC=3AE,BC=3BF,若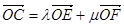 其中λ,μ∈R,则λ+μ是( )
其中λ,μ∈R,则λ+μ是( )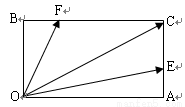
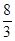 B.
B.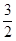
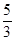 D.1
D.1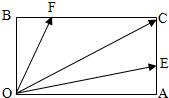
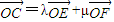 其中λ,μ∈R,则λ+μ是( )
其中λ,μ∈R,则λ+μ是( )