题目内容
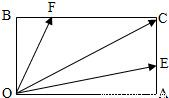
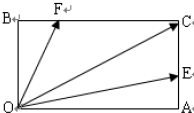 如图,在矩形OACB中,E和F分别是边AC和BC上的点,满足AC=3AE,BC=3BF,若
如图,在矩形OACB中,E和F分别是边AC和BC上的点,满足AC=3AE,BC=3BF,若| OC |
| OE |
| OF |
| 3 |
| 2 |
| 3 |
| 2 |
分析:根据平面向量的线性运算法则,得
=
+
且
=
+
,两式相加得
+
=
,从而得
=
+
,结合题意得到λ=μ=
,得λ+μ=
.
| OE |
| 2 |
| 3 |
| OA |
| 1 |
| 3 |
| OC |
| OF |
| 2 |
| 3 |
| OB |
| 1 |
| 3 |
| OC |
| OE |
| OF |
| 4 |
| 3 |
| OC |
| OC |
| 3 |
| 4 |
| OE |
| 3 |
| 4 |
| OF |
| 3 |
| 4 |
| 3 |
| 2 |
解答:解:∵
=3
,∴
-
=3(
-
),
整理得
=
+
,同理可得
=
+
,
∴
+
=
(
+
)+
,
∵矩形OABC中,
+
=
∴
+
=
,得
=
+
∵已知
=λ
+μ
,
∴λ=μ=
,得λ+μ=
故答案为:
| AC |
| AE |
| OC |
| OA |
| OE |
| OA |
整理得
| OE |
| 2 |
| 3 |
| OA |
| 1 |
| 3 |
| OC |
| OF |
| 2 |
| 3 |
| OB |
| 1 |
| 3 |
| OC |
∴
| OE |
| OF |
| 2 |
| 3 |
| OA |
| OB |
| 2 |
| 3 |
| OC |
∵矩形OABC中,
| OA |
| OB |
| OC |
∴
| OE |
| OF |
| 4 |
| 3 |
| OC |
| OC |
| 3 |
| 4 |
| OE |
| 3 |
| 4 |
| OF |
∵已知
| OC |
| OE |
| OF |
∴λ=μ=
| 3 |
| 4 |
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题给出矩形边的三等分点,求对角线对应向量的线性表达式,着重考查了平面向量的线性运算法则和平面向量的基本定理及其意义等知识点,属于中档题.

练习册系列答案
相关题目
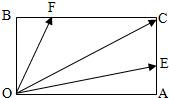 如图,在矩形OACB中,E和F分别是边AC和BC的点,满足AC=3AE,BC=3BF,若
如图,在矩形OACB中,E和F分别是边AC和BC的点,满足AC=3AE,BC=3BF,若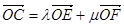 其中λ,μ∈R,则λ+μ是( )
其中λ,μ∈R,则λ+μ是( )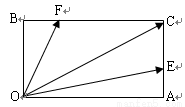
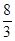 B.
B.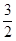
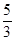 D.1
D.1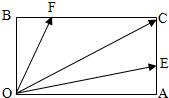
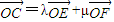 其中λ,μ∈R,则λ+μ是( )
其中λ,μ∈R,则λ+μ是( )