题目内容
若不等式
对一切正整数
都成立，求正整数
的最大值，并证明结论．
对一切正整数都成立，求正整数的最大值，并证明结论．的最大值等于25当
时，
，即
，
所以
．
而是正整数，所以取
，下面用数学归纳法证明：
．
（1）当时，已证；
（2）假设当
时，不等式成立，即
．
则当
时，
有
．
因为
，
所以，
所以
．
所以当时不等式也成立．
由（1）（2）知，对一切正整数，都有，
所以的最大值等于25．
时，，即，所以
．而
是正整数，所以取，下面用数学归纳法证明：．（1）当
时，已证；（2）假设当
时，不等式成立，即．则当
时，有
．因为
，所以
，所以
．所以当
时不等式也成立．由（1）（2）知，对一切正整数
，都有，所以
的最大值等于25．
练习册系列答案
相关题目
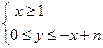表示的平面区域内可行解的个数，则f（1）=_______；f（2）=_______；f（n）=_______．
(an2+bn+c)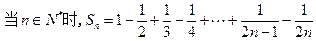
；
.
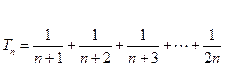
，由不等式
，启发我们归纳得到推广结论：
，其中
．
，则当n=k+1时左端应在n=k的基础上加上（ ）
