题目内容
18．点M （3，-2，1）关于平面yOz对称的点的坐标是（ ）| A． | （-3，-2，1 ） | B． | （-3，2，-1） | C． | （-3，-2，-1） | D． | （-3，2，1） |
分析 点M（a，b，c）关于平面yOz对称的点的坐标是（-a，b，c）．
解答 解：由空间直角坐标系的性质知：
点M （3，-2，1）关于平面yOz对称的点的坐标是（-3，-2，1）．
故选：A．
点评 本题考查点的坐标的求法，是基础题，解题时要认真审题，注意空间直角坐标系的性质的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
8．某交警大队对辖区A路段在连续10天内的n天，对过往车辆驾驶员进行血液酒精浓度检查，查得驾驶员酒驾率f（n）如表；
可用线性回归模型拟合f（n）与n的关系．
（1）建立f（n）关于n的回归方程；
（2）该交警大队将在2016年12月11日至20日和21日至30日对A路段过往车辆驾驶员进行血液酒精浓度检查，分别检查n1，n2天，其中n1，n2都是从8，9，10中随机选择一个，用回归方程结果求两阶段查得的驾驶员酒驾率都不超过0.03的概率．
附注：
参考数据：$\sum_{n=5}^9{nf（n）=1.51}$，$\sum_{n=5}^9{{n^2}=255}$，$\overline{f（n）}$=0.046，回归方程$\widehat{f（n）}$=$\widehat{b}$n+$\widehat{a}$中斜率和截距最小乘估计公式分别为：$\widehatb=\frac{{\sum_{n=5}^9{nf（n）-5\overline{nf（n）}}}}{{\sum_{n=5}^9{{n^2}-5{{\overline n}^2}}}}$，$\widehata=\overline{f（n）}$-$\widehatb\overline n$．
| n | 5 | 6 | 7 | 8 | 9 |
| f（n） | 0.06 | 0.06 | 0.05 | 0.04 | 0.02 |
（1）建立f（n）关于n的回归方程；
（2）该交警大队将在2016年12月11日至20日和21日至30日对A路段过往车辆驾驶员进行血液酒精浓度检查，分别检查n1，n2天，其中n1，n2都是从8，9，10中随机选择一个，用回归方程结果求两阶段查得的驾驶员酒驾率都不超过0.03的概率．
附注：
参考数据：$\sum_{n=5}^9{nf（n）=1.51}$，$\sum_{n=5}^9{{n^2}=255}$，$\overline{f（n）}$=0.046，回归方程$\widehat{f（n）}$=$\widehat{b}$n+$\widehat{a}$中斜率和截距最小乘估计公式分别为：$\widehatb=\frac{{\sum_{n=5}^9{nf（n）-5\overline{nf（n）}}}}{{\sum_{n=5}^9{{n^2}-5{{\overline n}^2}}}}$，$\widehata=\overline{f（n）}$-$\widehatb\overline n$．
6．对任意非零实数a、b，若a?b的运算原理如图所示，则（log28）?（$\frac{1}{2}$）2=（ ）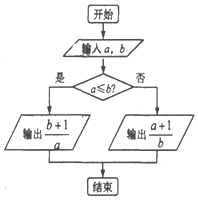 
| A． | 16 | B． | 15 | C． | 14 | D． | 13 |
在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市A（看做一点）的东偏南θ角方向$（{cosθ=\frac{{\sqrt{2}}}{10}}）$，300km的海面P处，并以20km/h的速度向西偏北45°方向移动．台风侵袭的范围为圆形区域，当前半径为60km，并以10km/h的速度不断增大．