题目内容
已知AB=2,BC=1的矩形ABCD,沿对角线BD将△BDC折起得到三棱锥E-ABD,且三棱锥的体积为
,则二面角E-BD-A的正弦值为
.
| ||
| 15 |
| 1 |
| 2 |
| 1 |
| 2 |
分析:利用三棱锥的体积求出E到平面ABD的距离,过E作EF⊥BD,连接OF,则∠EFO为二面角E-BD-A的平面角,从而可求二面角E-BD-A的正弦值.
解答: 解:设E到平面ABD的距离为EO=h,则由题意,
解:设E到平面ABD的距离为EO=h,则由题意,
∵三棱锥的体积为
,∴
=
×
×2×1×h
∴h=
,
过E作EF⊥BD,连接OF,则OF⊥BD,∴∠EFO为二面角E-BD-A的平面角
在Rt△EBD中,EF=
=
∴sin∠EFO=
=
=
故答案为:
 解:设E到平面ABD的距离为EO=h,则由题意,
解:设E到平面ABD的距离为EO=h,则由题意,∵三棱锥的体积为
| ||
| 15 |
| ||
| 15 |
| 1 |
| 3 |
| 1 |
| 2 |
∴h=
| ||
| 5 |
过E作EF⊥BD,连接OF,则OF⊥BD,∴∠EFO为二面角E-BD-A的平面角
在Rt△EBD中,EF=
| EB×ED |
| BD |
| 2 | ||
|
∴sin∠EFO=
| EO |
| EF |
| ||||
|
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查面面角,考查三棱锥体积的计算,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 如图所示的几何体中,四边形ABCD是矩形,平面ABCD⊥平面ABE,已知AB=2,BC=1,AE=BE=
如图所示的几何体中,四边形ABCD是矩形,平面ABCD⊥平面ABE,已知AB=2,BC=1,AE=BE=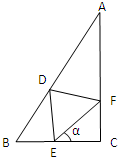 在△ABC中,已知AB=2,BC=1,CA=
在△ABC中,已知AB=2,BC=1,CA=