Question

在△ABC中，已知AB=2，BC=1，CA=

3

，分别在边AB、BC、CA上取点D、E、F，使△DEF是等边三角形（如图）．设∠FEC=α，问sinα为何值时，△DEF的边长最小？并求出最小值．

Answer 1

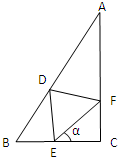
分析：设等边△DEF的边长为x，显然∠C=90°，∠B=60°，EC=x•cosα，得到∠EDB=α，在三角形BDE中，利用正弦定理列出关系式，表示出BE，由BE+EC=BC，列出关于x的方程，求出方程的解得到x的值，得到三角形的边长，求出边长的最小值，以及此时sinα的值即可．

解答：解：设等边△DEF的边长为x，显然∠C=90°，∠B=60°，EC=x•cosα，
∵∠DEC=∠DEF+α=∠EDB+∠B，
∴∠EDB=α．
在△BDE中，由正弦定理得

x

sin60°

=

BE

sinα

，
∴BE=

2 3

3

xsinα，
∵BE+EC=BC，∴xcosα+

2 3

3

xsinα=1，
∴x=

1

cosα+ 2 3 3 sinα

=

3

7( 2 7 sinα+ 3 7 cosα)

=

3

7 sin(α+θ)

．
当α+θ=

π

2

，即α=

π

2

-θ时，x_min=

21

7

，此时sinα=cosθ=

2 7

7

．

点评：此题考查了正弦定理，正弦函数的值域，以及两角和与差的正弦函数公式，熟练掌握正弦定理是解本题的关键．