题目内容
已知AB=2，BC=1的矩形ABCD，沿对角形BD将△BDC折起得到三棱锥C-ABD，且三棱锥的体积为2
| ||
| 15 |
分析：求出棱锥的高等于直角三角形BCD的斜边BD上的高，可得平面BCD⊥平面ABD，作CE⊥BD，AF⊥BD，利用两个向量的数量积的定义求出
•
的值，再根据又
•
=（
+
）•（
+
） 求出
•
的值，从而得到
cos＜
，
＞，即得BC与AD所成角的余弦值．
| AD |
| BC |
| AD |
| BC |
| AF |
| FD |
| BE |
| EC |
| AD |
| BC |
cos＜
| AD |
| BC |
解答：解：设三棱锥C-ABD的高为h，则
（
×2×1）h=
，∴h=
，
故 h是直角三角形BCD的斜边BD上的高，故平面BCD⊥平面ABD．作CE⊥BD，AF⊥BD，则
CE⊥面ABD，AF⊥面 BCD．
•
=1×1cos＜
，
＞=cos＜
，
＞．
又
•
=（
+
）•（
+
）=
•
+
•
+
•
+
•
=0+0+
2+0=BC2-CE2=1-(
)2=
，
∴cos＜
，
＞=
，故异面直线BC与AD所成角的余弦值为
，
故答案为
．
| 1 |
| 3 |
| 1 |
| 2 |
2
| ||
| 15 |
| 2 | ||
|
故 h是直角三角形BCD的斜边BD上的高，故平面BCD⊥平面ABD．作CE⊥BD，AF⊥BD，则
CE⊥面ABD，AF⊥面 BCD．
| AD |
| BC |
| AD |
| BC |
| AD |
| BC |
又
| AD |
| BC |
| AF |
| FD |
| BE |
| EC |
| AF |
| BE |
| AF |
| EC |
| FD |
| BE |
| FD |
| EC |
=0+0+
| FD |
| 2 | ||
|
| 1 |
| 5 |
∴cos＜
| AD |
| BC |
| 1 |
| 5 |
| 1 |
| 5 |
故答案为
| 1 |
| 5 |
点评：本题考查异面直线所成的角的定义和求法，体现了转化的数学的思想，求出cos＜
，
＞是解题的关键．
| AD |
| BC |
练习册系列答案
相关题目
如图所示的几何体中，四边形ABCD是矩形，平面ABCD⊥平面ABE，已知AB=2，BC=1，AE=BE=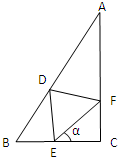
在△ABC中，已知AB=2，BC=1，CA=