Question

求适合下列条件的双曲线的标准方程：

(1)焦距为16，准线方程为y=±;

(2)虚轴长为12，离心率为;

(3)顶点间的距离为6，渐近线方程为y=±x.

Answer 1

剖析：要求双曲线的标准方程，首先判断其焦点所在的坐标轴，然后求其标准方程中待定的a和b.

解：(1)由准线方程为y=±，可知双曲线的焦点在y轴上.

设所求双曲线的方程为

    -=1(a＞0,b＞0).

    由题意，得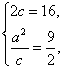解得a=6,c=8.

    所以b²=c²-a²=64-36=28.

    因此，所求双曲线的方程为-=1.

    (2)当焦点在x轴上时，设所求双曲线的方程为-=1.

    由题意，得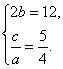

    解得b=6,c=a.

    ∴b²=c²-a²=a²=36,a=8.

    所以焦点在x轴上的双曲线的方程为-=1.

    同理可求焦点在y轴上的双曲线的方程为-=1.

    因此，所要求的双曲线的方程为-=1和-=1.

    (3)方法一：当焦点在x轴上时，设所求双曲线的方程为-=1.

    由题意，得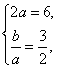解得a=3,b=.

    所以焦点在x轴上的双曲线的方程为-=1.

    同理可求焦点在y轴上的双曲线的方程为-=1.

    因此所求双曲线方程为-=1或-=1.

    方法二：设双曲线方程为-=λ(λ≠0).

    当λ＞0时，2=6,∴λ=.此时双曲线的方程为-=1.

    当λ＜0时，2-=6,∴λ=-1.此时双曲线方程为-=1.

讲评：本题考查双曲线方程，关键是求a、b,在解题过程中应熟悉各元素(a、b、c、e及准线)之间的关系，并注意方程思想的应用.若已知双曲线的渐近线方程ax±by=0，可设双曲线方程为a²x²-b²y²=λ(λ≠0).但要注意双曲线的焦点在哪条坐标轴上，不要漏解.