题目内容
在锐角△ABC中,BD、CE分别是边AC、AB上的高线,DG⊥CE于G,EF⊥BD于F.求证:FG∥BC.
思路分析:证FG∥BC,只需证∠DFG=∠DBC即可.我们设法由共斜边的两个直角三角形的四顶点共圆来分析角的关系,探求证明的思路.
证明:如图2-2-5,由于Rt△BCE与Rt△BCD共斜边BC,所以B、C、D、E四点共圆.由同弧上的圆周角,有∠DBC=∠DEG.
同理,Rt△EDF与Rt△DGE共斜边DE,所以D、E、F、G四点共圆.
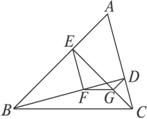
图2-2-5
于是,∠DEG=∠DFG.
因此,∠DBC=∠DFG.
于是FG∥BC.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 的取值范围是( )
的取值范围是( )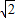 ,2)
,2)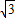 )
)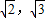 )
)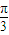 ,sin2A+sin(A-C)-sinB=0,则△ABC的面积为 .
,sin2A+sin(A-C)-sinB=0,则△ABC的面积为 .