题目内容
设抛物线以O为顶点,F为焦点,PQ是过焦点F的弦,已知｜OF｜=a,｜PQ｜=b,求△OPQ的面积.
思路分析：由本题条件｜PQ｜=b,求△OPQ的面积,易建立极坐标系.根据抛物线的极坐标方程的特点,可以把抛物线的焦点作为极点,以抛物线的对称轴为极轴建立极坐标系.
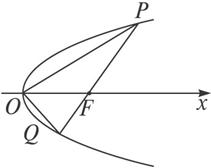
解：如图,以F为极点,抛物线的对称轴为极轴建立极坐标系.则抛物线的方程为
ρ=
.
设点P的极角为θ〔θ∈(0,π)〕,则点Q的极角为π+θ.
所以
｜PQ｜=ρP+ρQ=
,
即
=b.所以sinθ=
.
又S△OPF=
a·｜PF｜sinθ,S△OQF=
a｜FQ｜sinθ,
故S△OPQ=S△OPF+S△OQF=
a(｜FP｜+｜FQ｜)sinθ=
absinθ=
.
练习册系列答案
相关题目
轴上一点
，斜率为
，两端点A，B到
，