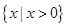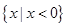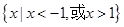题目内容
方程 的实根个数是( )
的实根个数是( )
| A.3 | B.2 | C.1 | D.0 |
C
解析试题分析:解:设 ,则
,则
令 即
即 ,解得:
,解得:
当变 化时,
化时,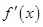 及
及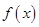 的变化情况如下表
的变化情况如下表
由表可知当

-1 
5 
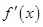
+ 0 - 0 + 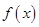
单调递增 -2 单调递减 -110 单调递增  时,
时, ,
,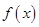 在
在 上为增函数,且
上为增函数,且
所以函数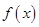 有唯一零点.所以方程
有唯一零点.所以方程 有且只有一个实根.故选C.
有且只有一个实根.故选C.
考点:1 利用导数研究函数的性质;2、函数的零点.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
若 则f′(x)
则f′(x) 的解集为( )
的解集为( )
A.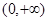 | B.(-1,0)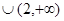 | C. | D.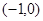 |
函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,
则f(x)>2x+4的解集为 ( ).
| A.(-1,1) | B.(-1,+∞) |
| C.(-∞,-1) | D.(-∞,+∞) |
已知函数y=f(x)的图象关于y轴对称,且当x∈(-∞,0)时,f(x)+xf′(x)<0成立,a=(20.2)·f(20.2),b=(logπ3)·f(logπ3),c=(log39)·f(log39),则a,b,c的大小关系是( )
| A.b>a>c | B.c>a>b |
| C.c>b>a | D.a>c>b |
函数y=2x3+1的图象与函数y=3x2-b的图象有三个不相同的交点,则实数b的取值范围是( )
| A.(-2,-1) | B.(-1,0) |
| C.(0,1) | D.(1,2) |
设函数f(x)的导函数为f′(x),对任意x∈R都有f′(x)>f(x)成立,则( )
| A.3f(ln 2)>2f(ln 3) | B.3f(ln 2)=2f(ln 3) |
| C.3f(ln 2)<2f(ln 3) | D.3f(ln 2)与2f(ln 3)的大小不确定 |


 x3+ax2+(a2-1)x+1(a∈R,a≠0)的导函数f′(x)的图象,则f(-1)为( )
x3+ax2+(a2-1)x+1(a∈R,a≠0)的导函数f′(x)的图象,则f(-1)为( )