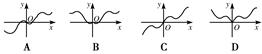题目内容
函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,
则f(x)>2x+4的解集为 ( ).
| A.(-1,1) | B.(-1,+∞) |
| C.(-∞,-1) | D.(-∞,+∞) |
B
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数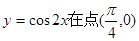 处的切线方程是
处的切线方程是
A.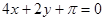 | B.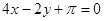 | C.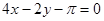 | D.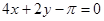 |
方程 的实根个数是( )
的实根个数是( )
| A.3 | B.2 | C.1 | D.0 |
已知e为自然对数的底数,则函数y=xex的单调递增区间是( )
| A.[-1,+∞) | B.(-∞,-1] |
| C.[1,+∞) | D.(-∞,1] |
设函数f(x)的定义域为R,x0(x0≠0)是f(x)的极大值点,以下结论一定正确的是( )
| A.?x∈R,f(x)≤f(x0) |
| B.-x0是f(-x)的极小值点 |
| C.-x0是-f(x)的极小值点 |
| D.-x0是-f(-x)的极小值点 |
已知f(x)=sin x-cos x,则f′ 等于 ( ).
等于 ( ).
| A.0 | B. | C. | D.1 |
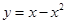 与x轴所围成的平面区域为
与x轴所围成的平面区域为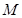 ,该抛物线与直线y=
,该抛物线与直线y=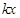 (k>0)所围成的平面区域为
(k>0)所围成的平面区域为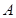 ,向区域
,向区域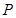 ,若点
,若点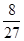 ,则k的值为( )
,则k的值为( )
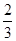
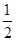
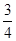
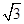 ),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )
),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )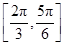
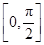 ∪
∪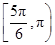
 ∪
∪
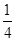 x2+
x2+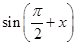 ,f′(x)为f(x)的导函数,则f′(x)的图象是( )
,f′(x)为f(x)的导函数,则f′(x)的图象是( )