题目内容
设数列{an}的前n项和为Sn,且满足Sn=2-an,n N*
N*
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{ b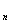 }满足b
}满足b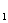 =1,且b
=1,且b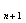 = b
= b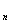 +a
+a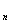 ,求数列{ b
,求数列{ b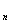 }的通项公式;
}的通项公式;
(Ⅲ)设cn=n(3- b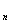 ),求数列{ cn}的前n项和Tn.
),求数列{ cn}的前n项和Tn.
(1)a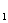 =S
=S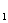 =1 n≥2时,S
=1 n≥2时,S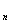 =2- a
=2- a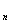 S
S =2- a
=2- a
 a
a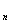 = - a
= - a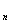 + a
+ a 2 a
2 a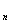 = a
= a ∵a
∵a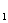 =1
=1

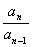 =
=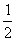
∴a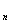 =(
=(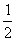 )
)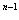 ……4分
……4分
(2)b -b
-b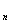 =(
=(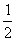 )
)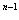
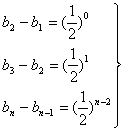
∴b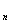 -b
-b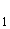 = (
= (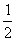 )0+……+(
)0+……+(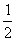 )
)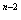
=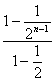
=2-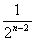
∴b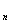 =3-
=3-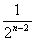
∵b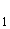 =1 成立
=1 成立
∴b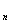 =3-(
=3-(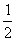 )
)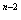 …………9分
…………9分
(3)c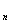 =n(
=n(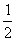 )
)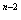
T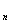 =1×(
=1×(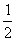 )
)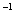 +2(
+2(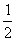 )
)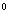 +……+n(
+……+n(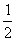 )
)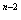
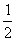 T
T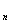 =1×(
=1×(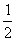 )
)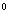 +……+(n-1) (
+……+(n-1) (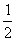 )
)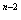 +n(
+n(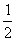 )
)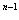

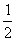 T
T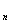 =2+
=2+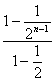 -n(
-n(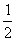 )
)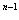
=2+2-(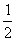 )
)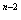 -n(
-n(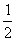 )
)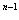
∴T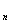 =8-
=8-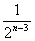 -
- =8-
=8- ……………………………………14分
……………………………………14分

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
 ,已知函数
,已知函数 (
( )至少有5个零点,则
)至少有5个零点,则 的取值范围为 .
的取值范围为 . 
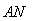 =
=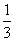
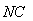 ,P是BN上的一点,若
,P是BN上的一点,若 ,则实数
,则实数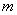 的值为
的值为 B.
B. 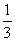 C. 1 D.3
C. 1 D.3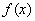 满足
满足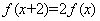 ,当
,当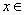 [0,2)时,
[0,2)时,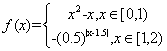 若
若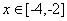 时,
时,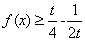 恒成立,则实数t的取值范围是______________.
恒成立,则实数t的取值范围是______________. 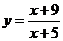 相切的直线方程是 ( )
相切的直线方程是 ( )
 或
或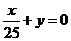 B
B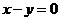 或
或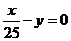 D
D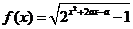 的值域为
的值域为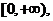 则实数
则实数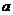 的取值范围是
的取值范围是
 ____________
____________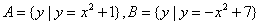 ,则
,则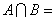 _____.
_____.