题目内容
设函数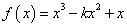
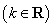 .
.
(1)当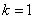 时,求函数
时,求函数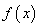 的单调区间;
的单调区间;
(2) 当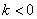 时,求函数
时,求函数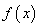 在
在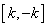 上的最小值
上的最小值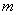 和最大值
和最大值 .
.
【解析】(1)当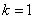 时,
时,  ,
,
∵ ,∴
,∴ 在
在 上恒成立,∴
上恒成立,∴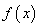 在
在 上单调递增.
上单调递增.
∴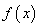 的单调递增区间为
的单调递增区间为 ,无递减区间.
,无递减区间.
(2)  ,判别式
,判别式
当 ,即
,即 时,
时, 在
在 上恒成立,∴
上恒成立,∴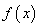 在
在 上单调递增.
上单调递增.
 ∴
∴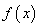 在
在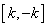 上的最小值
上的最小值 ,最大值
,最大值 ;
;
当 ,即
,即 时,
时,
令 得
得 ,
, .
.
∵ 的对称轴为
的对称轴为 ,且恒过
,且恒过 ,
,
画出大致图像如图所示,可知 ,
,
当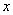 变化时,
变化时, ,
,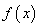 的变化如下表:
的变化如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
| 极大值 |
| 极小值 |
|
|
由表可知, ,
, .
.
∵ ,∴
,∴ .
.
∵ ,
,
∴ .
.
综上所述,当 时,函数
时,函数 在
在 上的最小值
上的最小值 ,最大值
,最大值 .
.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目













 元时,销售量可达到
元时,销售量可达到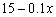 万套.现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10.假设不计其它成本,即销售每套丛书的利润
万套.现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10.假设不计其它成本,即销售每套丛书的利润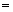 售价
售价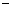 供货价格.问:
供货价格.问: 在
在 处取到极值,则
处取到极值,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 有零点,则
有零点,则 的取值范围是
的取值范围是  在
在 处取得极值.
处取得极值.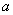 的值; (2)求证:对任意
的值; (2)求证:对任意 ,都有
,都有 .
. ;
; ,若曲线
,若曲线 与直线
与直线 相切于点
相切于点 ,求
,求 的解析式
的解析式 满足
满足 ,
, ,求
,求