题目内容
若空间两点A（m，n，1）、A′（n-1，2-m，1）关于z轴对称，则mn的值为
-
| 3 |
| 4 |
-
．| 3 |
| 4 |
分析：在空间直角坐标系中，A（m，n，1）、A′（n-1，2-m，1）关于z轴对称就是把x变为-x，y变为-y，z不变，从而q求出m，n，即可求解；
解答：解：∵在空间直角坐标系中，A（m，n，1）、A′（n-1，2-m，1）关于z轴对称，
∴
，解得m=
，n=-
，mn=-
．
故答案为：-
；
∴
|
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
故答案为：-
| 3 |
| 4 |
点评：此题主要考查空间直角坐标系，点的对称问题，点（x，y，z）关于z轴对称为（-x，-y，z）是解题的关键，是一道基础题．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
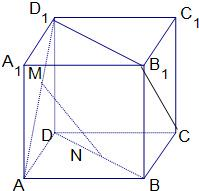如图ABCD-A1B1C1D1是正方体，M、N分别是线段AD1和BD上的中点
，BC=CD=a，AB=AD=
a，A在面BCD上的射影为A1，若AA1中点为M，BC中点为N，过A、B、C、D四点的球的球心为O，直线MN与球面交于P、Q两点，则∠POQ=_____________.
