题目内容
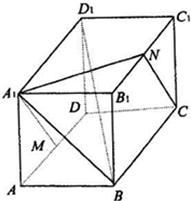
如图ABCD-A1B1C1D1是正方体,M、N分别是线段AD1和BD上的中点(Ⅰ)证明:直线MN∥平面B1D1C;
(Ⅱ)设正方体ABCD-A1B1C1D1棱长为a,若以D为坐标原点,分别以DA,DC,DD1所在的直线为x轴、y轴、z轴,建立空间直角坐标系,试写出B1、M两点的坐标,并求线段B1M的长.

【答案】分析:(Ⅰ)证明:连接CD1、AC、则N是AC的中点,由三角形中位线证得MN∥CD1,从而由线面平行的判定定理证得直线MN∥平面B1D1C;(Ⅱ)先求得各点的坐标,再由两点间的距离公式求解.
解答: 证明:(Ⅰ)证明:连接CD1、AC、则N是AC的中点(2分)
证明:(Ⅰ)证明:连接CD1、AC、则N是AC的中点(2分)
在△ACD1,又M是AD1的中点
∴MN∥CD1,又CD1?平面ACD1.(3分)∴MN∥平面ADC1.(5分)
(Ⅱ)B1(a,a,a),M( ,0,
,0, )(8分)
)(8分) (10分)
(10分)
点评:本题主要考查空间线线、线面、面面位置平行关系转化,空间直角坐标系的概念与运算等基础知识,同时考查空间想象能力和推理运算能力.
解答:
 证明:(Ⅰ)证明:连接CD1、AC、则N是AC的中点(2分)
证明:(Ⅰ)证明:连接CD1、AC、则N是AC的中点(2分)在△ACD1,又M是AD1的中点
∴MN∥CD1,又CD1?平面ACD1.(3分)∴MN∥平面ADC1.(5分)
(Ⅱ)B1(a,a,a),M(
 ,0,
,0, )(8分)
)(8分) (10分)
(10分)点评:本题主要考查空间线线、线面、面面位置平行关系转化,空间直角坐标系的概念与运算等基础知识,同时考查空间想象能力和推理运算能力.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 如图,在正方体ABCD-A1B1C1D1中,棱长为a,M、N分别为A1B和AC上的点,A1M=AN=
如图,在正方体ABCD-A1B1C1D1中,棱长为a,M、N分别为A1B和AC上的点,A1M=AN=
| ||
| 3 |
| A、相交 | B、平行 |
| C、垂直 | D、不能确定 |
 如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC=
如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC=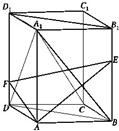 如图,在长方体ABCD-A1B1C1D1中,点E、F分别BB1、DD1上,且AE⊥A1B,AF⊥A1D.
如图,在长方体ABCD-A1B1C1D1中,点E、F分别BB1、DD1上,且AE⊥A1B,AF⊥A1D. 如图,在正方体ABCD-A1B1C1D1中,直线A1B与平面A1B1CD所成的角的大小等于
如图,在正方体ABCD-A1B1C1D1中,直线A1B与平面A1B1CD所成的角的大小等于 (2007•无锡二模)如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD为直角梯形,AB∥CD,AB⊥AD,AB=AD=A1B=2CD,侧面A1ADD1为正方形.
(2007•无锡二模)如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD为直角梯形,AB∥CD,AB⊥AD,AB=AD=A1B=2CD,侧面A1ADD1为正方形.