题目内容
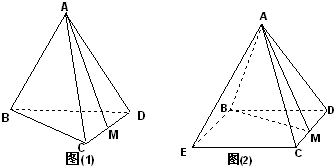 正四面体A-BCD的棱长为1,(Ⅰ)如图(1)M为CD中点,求异面直线AM与BC所成的角;(Ⅱ)将正四面体沿AB、BD、DC、BC剪开,作为正四棱锥的侧面如图(2),求二面角M-AB-E的大小;(Ⅲ)若将图(1)与图(2)面ACD重合,问该几何体是几面体(不需要证明),并求这几何体的体积.
正四面体A-BCD的棱长为1,(Ⅰ)如图(1)M为CD中点,求异面直线AM与BC所成的角;(Ⅱ)将正四面体沿AB、BD、DC、BC剪开,作为正四棱锥的侧面如图(2),求二面角M-AB-E的大小;(Ⅲ)若将图(1)与图(2)面ACD重合,问该几何体是几面体(不需要证明),并求这几何体的体积.
分析:(Ⅰ)求异面直线AM与BC所成的角,得先作出其平面角来,由图取BD中点N.连AN、MN,可证得∠AMN就是异面直线AM与BC所成的角,在三角形中求解;
(Ⅱ)先作二面角M-AB-E的平面角,取BE中点P.连AP、PM,作MQ⊥AP于Q.过Q作QH⊥AB于H.连MH可证得∠MHQ为二面角M-AB-E的平面角,在所组成的三角形中求角;
(Ⅲ)根据题设中的要求,及图形得出是五面体,再由体积公式求得出体积即可.
(Ⅱ)先作二面角M-AB-E的平面角,取BE中点P.连AP、PM,作MQ⊥AP于Q.过Q作QH⊥AB于H.连MH可证得∠MHQ为二面角M-AB-E的平面角,在所组成的三角形中求角;
(Ⅲ)根据题设中的要求,及图形得出是五面体,再由体积公式求得出体积即可.
解答:解:(Ⅰ)取BD中点N.连AN、MN.
∵MN∥BC
∴∠AMN就是异面直线AM与BC所成的角,在△AMN中,
AM=AN=
,MN=
∴∠AMN=arccos
(4分)
(Ⅱ)取BE中点P.连AP、PM,作MQ⊥AP于Q.过Q作QH⊥AB于H.连MH.
∵EB⊥AP,EB⊥PM
∴EB⊥面APM即EB⊥MQ,
∴MQ⊥面AEB
∴HQ为MH在面AEB上的射影.,即MH⊥AB
∴∠MHQ为二面角M-AB-E的平面角,
在△AMP中,AM=AP=
,PM=1,MQ=
,PQ=
在△ABP中,AQ=AP-PQ=
-
,AQ=
,HQ=
∴∠MHQ=arctan4
∴二面角M-AB-E的大小,为arctan4
(8分)
(Ⅲ)若将图(1)与图(2)面ACD重合,该几何体是7面体 (9分)
体积=3VA-BCD=3×
×
×
=
(12分)
∵MN∥BC
∴∠AMN就是异面直线AM与BC所成的角,在△AMN中,
AM=AN=
| ||
| 2 |
| 1 |
| 2 |
∴∠AMN=arccos
| ||
| 6 |
(Ⅱ)取BE中点P.连AP、PM,作MQ⊥AP于Q.过Q作QH⊥AB于H.连MH.
∵EB⊥AP,EB⊥PM
∴EB⊥面APM即EB⊥MQ,
∴MQ⊥面AEB
∴HQ为MH在面AEB上的射影.,即MH⊥AB
∴∠MHQ为二面角M-AB-E的平面角,
在△AMP中,AM=AP=
| ||
| 2 |
| ||
| 3 |
| ||
| 3 |
在△ABP中,AQ=AP-PQ=
| ||
| 2 |
| ||
| 3 |
| ||
| 3 |
| ||
| 12 |
∴∠MHQ=arctan4
| 2. |
| 2. |
(Ⅲ)若将图(1)与图(2)面ACD重合,该几何体是7面体 (9分)
体积=3VA-BCD=3×
| 1 |
| 3 |
| ||
| 4 |
| ||
| 3 |
| ||
| 4 |
点评:本题考查棱柱、棱锥、棱台的体积,解题的关键是有较好的空间立体感知能力,对所给的几何体对应的实物图能想像出来,本题知识性较强,要掌握好异面直线所成的角,二面角的作法,以及多面体的体积求法

练习册系列答案
相关题目
若点P是正四面体A-BCD的面BCD上一点,且P到另三个面的距离分别为h1,h2,h3,正四面体A-BCD的高为h,则( )
| A、h>h1+h2+h3 | B、h=h1+h2+h3 | C、h<h1+h2+h3 | D、h1,h2,h3与h的关系不定 |
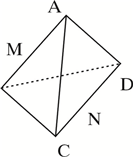 如图,正四面体A-BCD的棱长为
如图,正四面体A-BCD的棱长为