题目内容
若点P是正四面体A-BCD的面BCD上一点，且P到另三个面的距离分别为h1，h2，h3，正四面体A-BCD的高为h，则（ ）
| A、h＞h1+h2+h3 | B、h=h1+h2+h3 | C、h＜h1+h2+h3 | D、h1，h2，h3与h的关系不定 |
分析：由VA-BCD=VP-ABC+VP-ACD+VP-ABD，可得
S•h=
S•h1+
S•h2+
S•h3，即可得h=h1+h2+h3，从而得到结论．
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解答：解：VA-BCD=VP-ABC+VP-ACD+VP-ABD，结合正四面体A-BCD的四个面的面积相等
可得
S•h=
S•h1+
S•h2+
S•h3，
即可得h=h1+h2+h3
∴h=h1+h2+h3；
故选B．
可得
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
即可得h=h1+h2+h3
∴h=h1+h2+h3；
故选B．
点评：此题考查了正四面体和棱锥的体积的求解方法．此题难度适中，解题的关键是将体积进行等价转化，属于中档题．
练习册系列答案
相关题目
若点P是正四面体A－BCD的面BCD上一点，且P到另三个面的距离分别为
h1，h2，h3，正四面体A－BCD的高为h，则( )
A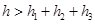． | B．h＝h1＋h2＋h3 |
C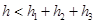． | D．h1，h2，h3与h的关系不定 |
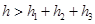B．h＝h1＋h2＋h3
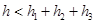D．h1，h2，h3与h的关系不定