Question

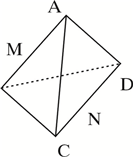如图，正四面体A-BCD的棱长为2

2

，且M，N分别为AB、CD的中点．
（1）求MN和BD所成角的大小；
（2）求BN与DM所成角的大小；
（3）求该四面体的外接球的体积．

Answer 1

分析：把正四面体A-BCD放入如图正方体中，则正方体棱长为2．以A为原点建立坐标系求出个顶点坐标，
（1）得到

MN

，

BD

的坐标，再代入向量夹角的计算公式即可求出结论；
（2）得到

BN

，

DM

的坐标，再代入向量夹角的计算公式即可求出结论；
（3）根据正四面体的外接球就是正方体的外接球，而且正方体的对角线长为2

3

，就是外接球的直径即可求出四面体的外接球的体积．

解答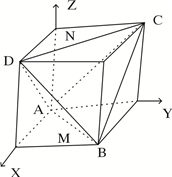：解：把正四面体A-BCD放入如图正方体中，则正方体棱长为2．以A为原点建立坐标系，则A（0，0，0，），B（2，2，0）M（1，1，0），D（2，0，2），N（1，1，2）．
（1）∵

MN

=(0，0，2)，

BD

=(0，-2，2)．
∴cos?

MN

，

BD

＞=

4

2•2 2

=

2

2

，、
∴MN和BD所成角的大小为

π

4

．
（2）∵

BN

=(-1，-1，2)，

MD

=(1，-1，2)．
∴cos?

BN

，

MD

＞=

4

6 • 6

=

2

3

．
∴BN与DM所成角大小为arccos

2

3

．
（3）该正四面体的外接球就是正方体的外接球，正方体的对角线长为2

3

，就是外接球的直径，
∴外接球的半径为

3

，体积为4

3

π．

点评：本题主要考察用空间向量求直线间的夹角、距离．在处理空间问题不好解决时，常常把他们放在空间几何体中来直观的分析，正方体是最常用的空间模型，大家一定要熟练掌握这种方法．