题目内容
各项均为正数的数列{an}的前n项和为Sn,且点(an,Sn)在函数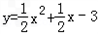 的图象上,
的图象上,
(1)求数列{an}的通项公式;
(2)记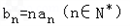 ,求证:
,求证: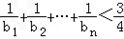 .
.
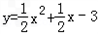 的图象上,
的图象上,(1)求数列{an}的通项公式;
(2)记
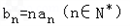 ,求证:
,求证: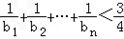 .
.(1)解:∵点(an,Sn)在函数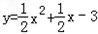 的图象上,
的图象上,
∴Sn= an2+
an2+ an﹣3;Sn﹣1=
an﹣3;Sn﹣1= an﹣12+
an﹣12+ an﹣1﹣3(n≥2)
an﹣1﹣3(n≥2)
∵Sn﹣Sn﹣1=an,
∴(an+an﹣1)(an﹣an﹣1﹣1)=0
∵数列{an}各项均为正数
∴an﹣an﹣1﹣1=0(n≥2)
∴数列{an}为等差数列
∵S1=a1= a12+
a12+ a1﹣3
a1﹣3
∴a1=3
∴an=a1+(n﹣1)d=2+n
(2)证明:bn=nan=n(n+2)
∴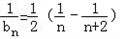
∴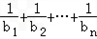 =
=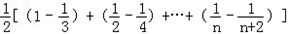
=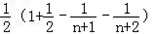 <
<
∴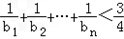 .
.
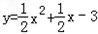 的图象上,
的图象上,∴Sn=
 an2+
an2+ an﹣3;Sn﹣1=
an﹣3;Sn﹣1= an﹣12+
an﹣12+ an﹣1﹣3(n≥2)
an﹣1﹣3(n≥2)∵Sn﹣Sn﹣1=an,
∴(an+an﹣1)(an﹣an﹣1﹣1)=0
∵数列{an}各项均为正数
∴an﹣an﹣1﹣1=0(n≥2)
∴数列{an}为等差数列
∵S1=a1=
 a12+
a12+ a1﹣3
a1﹣3∴a1=3
∴an=a1+(n﹣1)d=2+n
(2)证明:bn=nan=n(n+2)
∴
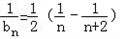
∴
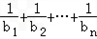 =
=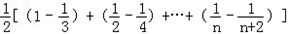
=
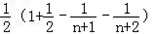 <
<
∴
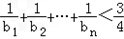 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目