题目内容
4.已知f(m)=${∫}_{0}^{m}$(x-2)dx≥0恒成立,求m的取值范围.分析 根据函数的积分公式进行计算,再得到关于m的不等式,解得即可
解答 解:∵${∫}_{0}^{m}$(x-2)dx=($\frac{1}{2}$x2-2x)|${\;}_{0}^{m}$=$\frac{1}{2}$m2-2m,f(m)=${∫}_{0}^{m}$(x-2)dx≥0恒成立,
∴$\frac{1}{2}$m2-2m≥0很成立,且m≥0,
解得m≥4或m=0,
故m的取值范围为{m|m≥4或m=0}.
点评 本题主要考查函数积分的计算和不等式的解法,属于基础题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
 如图,AB是圆的直径,C是圆上的点,且PA⊥BC.
如图,AB是圆的直径,C是圆上的点,且PA⊥BC.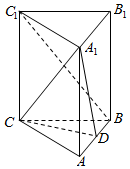 在三棱柱ABC-A1B1C1中,底面三角形ABC是等边三角形,侧棱AA1⊥底面ABC,D为棱AB的中点
在三棱柱ABC-A1B1C1中,底面三角形ABC是等边三角形,侧棱AA1⊥底面ABC,D为棱AB的中点