Question

【题目】在参加某次社会实践的学生中随机选取名学生的成绩作为样本，这名学生的成绩全部在分至分之间，现将成绩按如下方式分成组：第一组，成绩大于等于分且小于分；第二组，成绩大于等于分且小于分；第六组，成绩大于等于分且小于等于分，据此绘制了如图所示的频率分布直方图．在选取的名学生中．

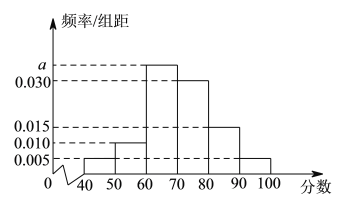
（Ⅰ）求的值及成绩在区间内的学生人数．

（Ⅱ）从成绩小于分的学生中随机选名学生，求最多有名学生成绩在区间内的概率．

Answer 1

【答案】（1），6（2）

【解析】分析：(1)根据所有小长方形面积的和为1，求的值，根据频数等于总数与频率的乘积得成绩在区间内的学生人数．(2)先根据频率得，, 利用组合数求总事件数，再求两名学生都在事件数，最后根据古典概型概率公式求结果.

详解：

（Ⅰ）．

成绩在区间内的学生人数为．

（Ⅱ）有人，

有人，

两名学生都在概率为：

，

∴．