题目内容
(12分)双曲线的离心率等于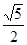 ,且与椭圆
,且与椭圆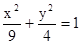 有公共焦点,
有公共焦点,
①求此双曲线的方程.
②若抛物线的焦点到准线的距离等于椭圆的焦距,求该抛物线方程.
【答案】
解:① ;②
;②


【解析】
试题分析:(1)因为双曲线的离心率可知a,c的关系式,然后利用其与椭圆有个公共的焦点,确定出c的值,进而求解得到其解析式。
(2)根据抛物线焦点到准线的距离为p,那么p=2c,得到求解,进而得到抛物线的方程。
解:① ∵  ,c=
,c= , ∴a=2,b=1
, ∴a=2,b=1
所以双曲线方程为
② 抛物线方程为

考点:本试题主要考查了双曲线方程的求解,以及抛物线方程的求解。
点评:解决该试题的关键是利用椭圆和双曲线以及抛物线的性质,找到对应的关系式,进而求解得到结论。

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
已知双曲线
-
=1(a>0)的中心在原点,右焦点与抛物线y2=16x的焦点重合,则该双曲线的离心率等于( )
| x2 |
| a2 |
| y2 |
| 9 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|