Question

（8分）求适合下列条件的双曲线的标准方程：

（1）  焦点在 x轴上,虚轴长为12，离心率为 ；

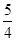（2） 顶点间的距离为6，渐近线方程为．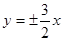

 

Answer 1

【答案】

（1）．

（2）焦点在x轴上的双曲线的方程为．

焦点在y轴上双曲线的方程为．

【解析】

试题分析：（1）焦点在x轴上，设所求双曲线的方程为=1．

由题意，得　解得，．　　∴．

所以焦点在x轴上的双曲线的方程为．

（2）当焦点在x轴上时，设所求双曲线的方程为=1

由题意，得　　　解得，　　．

所以焦点在x轴上的双曲线的方程为．

同理可求当焦点在y轴上双曲线的方程为．

考点：本题主要考查双曲线的标准方程及几何性质．

点评：关键是注意分类讨论焦点的可能情况，灵活运用双曲线的几何性质解决问题，对学生的运算能力有一定要求。