题目内容
已知四棱锥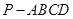 底面ABCD是矩形,PA⊥平面ABCD, AD=2,AB=1,E.F
底面ABCD是矩形,PA⊥平面ABCD, AD=2,AB=1,E.F
分别是线段AB.BC的中点,
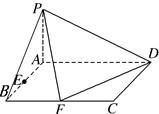
(1)证明:PF⊥FD;
(2)在PA上找一点G,使得EG∥平面PFD;.
(3)若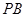 与平面
与平面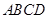 所成的角为
所成的角为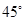 ,求二面角
,求二面角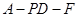 的余弦值.
的余弦值.
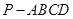 底面ABCD是矩形,PA⊥平面ABCD, AD=2,AB=1,E.F
底面ABCD是矩形,PA⊥平面ABCD, AD=2,AB=1,E.F分别是线段AB.BC的中点,

(1)证明:PF⊥FD;
(2)在PA上找一点G,使得EG∥平面PFD;.
(3)若
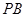 与平面
与平面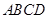 所成的角为
所成的角为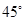 ,求二面角
,求二面角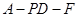 的余弦值.
的余弦值.(1)见解析(2)满足AG=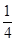 AP的点G为所求(3)
AP的点G为所求(3)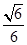
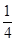 AP的点G为所求(3)
AP的点G为所求(3)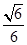
(1)证明FD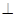 平面PAF即可.
平面PAF即可.
(2)取AD的四分之一分点N,使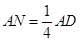 m则EN//DF,然后再取PA的四分之一分点,使
m则EN//DF,然后再取PA的四分之一分点,使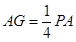 ,即是所求G点位置.易证EG//平面PFD.
,即是所求G点位置.易证EG//平面PFD.
(3)利用空间向量法求解即可.要把二面角两个面的法向量求出来,然后再求法向量的夹角.
解:(1)证明:连接AF,则AF=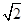 ,DF=
,DF=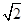 ,
,
又AD=2,∴DF2+AF2=AD2,∴DF⊥AF.又PA⊥平面ABCD,
∴DF⊥PA,又PA∩AF=A,
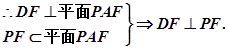 ……………4分
……………4分
(2)过点E作EH∥FD交AD于点H,则EH∥平面PFD且AH=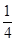 AD.
AD.
再过点H作HG∥DP交PA于点G,则HG∥平面PFD且AG=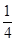 AP,
AP,
∴平面EHG∥平面PFD.∴EG∥平面PFD.
从而满足AG=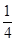 AP的点G为所求.………………8分
AP的点G为所求.………………8分
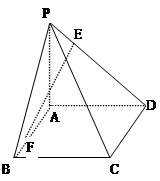
(3)建立如图所示的空间直角坐标系,
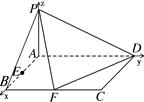
因为PA⊥平面ABCD ,所以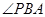 是
是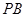 与平面
与平面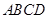 所成的角.又有已知得
所成的角.又有已知得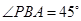 ,所以
,所以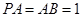 ,所以
,所以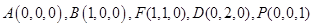 .
.
设平面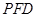 的法向量为
的法向量为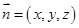 ,由
,由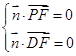
得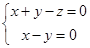 ,令
,令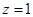 ,解得:
,解得: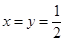 .
.
所以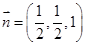 .又因为
.又因为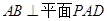 ,所以
,所以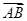 是平面
是平面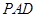 的法向量,易得
的法向量,易得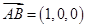 ,所以
,所以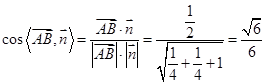 .
.
由图知,所求二面角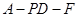 的余弦值为
的余弦值为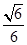 .……………………12分
.……………………12分
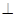 平面PAF即可.
平面PAF即可.(2)取AD的四分之一分点N,使
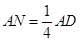 m则EN//DF,然后再取PA的四分之一分点,使
m则EN//DF,然后再取PA的四分之一分点,使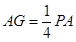 ,即是所求G点位置.易证EG//平面PFD.
,即是所求G点位置.易证EG//平面PFD.(3)利用空间向量法求解即可.要把二面角两个面的法向量求出来,然后再求法向量的夹角.
解:(1)证明:连接AF,则AF=
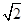 ,DF=
,DF=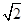 ,
,又AD=2,∴DF2+AF2=AD2,∴DF⊥AF.又PA⊥平面ABCD,
∴DF⊥PA,又PA∩AF=A,
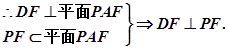 ……………4分
……………4分(2)过点E作EH∥FD交AD于点H,则EH∥平面PFD且AH=
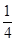 AD.
AD.再过点H作HG∥DP交PA于点G,则HG∥平面PFD且AG=
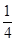 AP,
AP,∴平面EHG∥平面PFD.∴EG∥平面PFD.
从而满足AG=
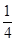 AP的点G为所求.………………8分
AP的点G为所求.………………8分(3)建立如图所示的空间直角坐标系,

因为PA⊥平面ABCD ,所以
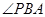 是
是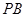 与平面
与平面 所成的角.又有已知得
所成的角.又有已知得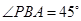 ,所以
,所以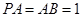 ,所以
,所以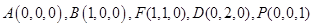 .
.设平面
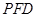 的法向量为
的法向量为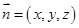 ,由
,由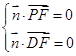
得
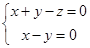 ,令
,令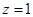 ,解得:
,解得: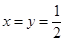 .
.所以
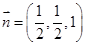 .又因为
.又因为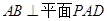 ,所以
,所以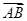 是平面
是平面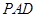 的法向量,易得
的法向量,易得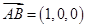 ,所以
,所以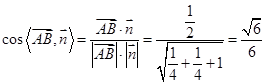 .
.由图知,所求二面角
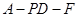 的余弦值为
的余弦值为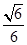 .……………………12分
.……………………12分
练习册系列答案
相关题目
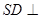 底面ABCD,底面ABCD是矩形,
底面ABCD,底面ABCD是矩形,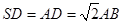 ,E是SA的中点.
,E是SA的中点.
 平面SAB;
平面SAB;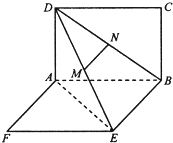
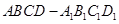 的棱长为
的棱长为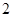 ,长为
,长为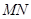 的一个端点
的一个端点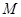 在棱
在棱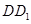 上运动,点
上运动,点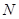 在正方形
在正方形 内运动,则
内运动,则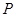 的轨迹的面积为( )
的轨迹的面积为( )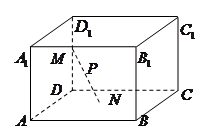
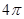
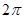
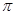
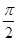
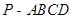 中,底面
中,底面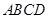 是矩形,
是矩形,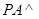 平面
平面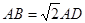 是线段
是线段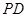 上的点,
上的点,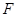 是线段
是线段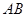 上的点,且
上的点,且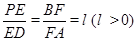
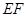 与平面
与平面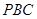 的关系,并证明;
的关系,并证明;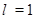 时,证明:面
时,证明:面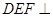 平面
平面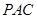 .
.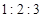
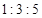
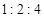
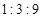
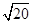
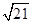
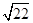
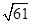
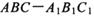 中,.
中,.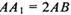 ,M为CC1的中点,则直线BM与平面
,M为CC1的中点,则直线BM与平面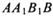 所成角的正弦值是_________.
所成角的正弦值是_________.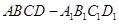 .则下列四个命题
.则下列四个命题
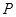 在直线
在直线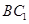 上运动时,三棱锥
上运动时,三棱锥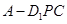 的体积不变;
的体积不变;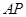 与平面
与平面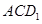 所成的角的大小不变;
所成的角的大小不变;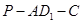 的大小不变;
的大小不变;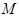 是平面
是平面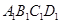 上到点
上到点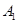 和
和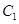 距离相等的点,则
距离相等的点,则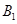
 ;
;