题目内容
3.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,过焦点垂直长轴的弦长为3.(1)求椭圆的标准方程;
(2)过椭圆的右顶点作直线交抛物线y2=2x于A、B两点,求证:OA⊥OB.
分析 (1)根据题意,分析可得$\left\{\begin{array}{l}\frac{c}{a}=\frac{1}{2}\\ \frac{{2{b^2}}}{a}=3\end{array}\right.$,解可得a、c的值,由椭圆的定义可得b的值,将a、b的值代入椭圆方程即可得答案;
(2)设过椭圆的右顶点(2,0)的直线AB的方程为x=my+2,与抛物线方程联立,设出A、B点的坐标,由根与系数的关系的关系分析计算x1x2+y1y2的值,由向量数量积的性质可得证明.
解答 解:(1)椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,过焦点垂直长轴的弦长为3,
则有$\left\{\begin{array}{l}\frac{c}{a}=\frac{1}{2}\\ \frac{{2{b^2}}}{a}=3\end{array}\right.$,
解可得a=2,c=1,则b2=a2-c2=3.
所以,所求椭圆的标准方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
(2)证明:设过椭圆的右顶点(2,0)的直线AB的方程为x=my+2.
代入抛物线方程y2=2x,得y2-2my-4=0.
设A(x1,y1)、B(x2,y2),
则$\left\{\begin{array}{l}{y_1}+{y_2}=2m\\{y_1}{y_2}=-4.\end{array}\right.$,
∴x1x2+y1y2=(my1+2)(my2+2)+y1y2=(1+m2)y1y2+2m(y1+y2)+4=0.
∴OA⊥OB.
点评 本题考查椭圆、抛物线的几何性质,涉及直线与椭圆、抛物线的位置关系,注意分析直线时需要讨论直线的斜率是存在.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案| A. | $\frac{1}{a}+\frac{1}{b}$有最大值4 | B. | $\sqrt{ab}$有最小值 $\frac{1}{2}$ | C. | $\sqrt{a}+\sqrt{b}$有最大值$\sqrt{2}$ | D. | a2+b2有最小值$\frac{{\sqrt{2}}}{2}$ |
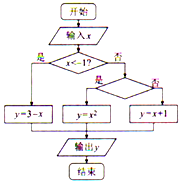 已知分段函数y=$\left\{\begin{array}{l}{3-x,x<-1}\\{{x}^{2},-1≤x≤1}\\{x+1,x>1}\end{array}\right.$,若执行如图所示的程序框图,则框图中的条件应该填写( )
已知分段函数y=$\left\{\begin{array}{l}{3-x,x<-1}\\{{x}^{2},-1≤x≤1}\\{x+1,x>1}\end{array}\right.$,若执行如图所示的程序框图,则框图中的条件应该填写( )| A. | x≥1? | B. | x≥-1? | C. | -1≤x≤2? | D. | x≤1? |
| A. | -2 | B. | -1 | C. | 2 | D. | $\frac{1}{2}$ |
| A. | 等边三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
| A. | $\sqrt{19}$ | B. | $\sqrt{13}$ | C. | 2 | D. | 1 |