题目内容
若函数f(x)=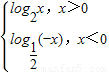 ,若f(a)>f(-a),则实数a的取值范围是( )
,若f(a)>f(-a),则实数a的取值范围是( )A.(-1,0)∪(0,1)
B.(-∞,-1)∪(1,+∞)
C.(-1,0)∪(1,+∞)
D.(-∞,-1)∪(0,1)
【答案】分析:由分段函数的表达式知,需要对a的正负进行分类讨论.
解答:解:由题意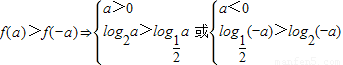
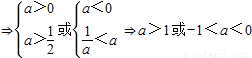
故选C.
点评:本题主要考查函数的对数的单调性、对数的基本运算及分类讨论思想,属于中等题.
分类函数不等式一般通过分类讨论的方式求解,解对数不等式既要注意真数大于0,
也要注意底数在(0,1)上时,不等号的方向不要写错.
解答:解:由题意
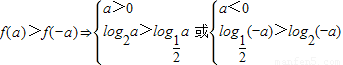
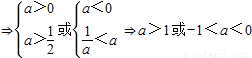
故选C.
点评:本题主要考查函数的对数的单调性、对数的基本运算及分类讨论思想,属于中等题.
分类函数不等式一般通过分类讨论的方式求解,解对数不等式既要注意真数大于0,
也要注意底数在(0,1)上时,不等号的方向不要写错.

练习册系列答案
相关题目
若函数f(x)满足条件:当x1,x2∈[-1,1]时,有|f(x1)-f(x2)|≤3|x1-x2|成立,则称f(x)∈Ω.对于函数g(x)=x3,h(x)=
,有( )
| 1 |
| x+2 |
| A、g(x)∈Ω且h(x)∉Ω |
| B、g(x)∉Ω且h(x)∈Ω |
| C、g(x)∈Ω且h(x)∈Ω |
| D、g(x)∉Ω且h(x)∉Ω |