题目内容

△ABC内角A，B，C的对边分别是a，b，c，若 $数学公式$ ， $数学公式$ ，则A=________．

$\text{[math]}$
分析：由正弦定理化简已知的等式，得到关于a，b及c的关系式，然后再利用余弦定理表示出cosA，把得到的关系式代入求出cosA的值，由A为三角形的内角，利用特殊角的三角函数值即可求出A的度数．
解答：根据正弦定理 $\text{[math]}$
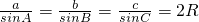
A化简已知等式得：
a²-b²= $\text{[math]}$ bc，
∵ $\text{[math]}$ ，
∴cosA= $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ，
又A为三角形的内角，
则A= $\text{[math]}$ ．
故答案为： $\text{[math]}$ ．
点评：此题考查了正弦定理，以及余弦定理的运用，熟练掌握定理是解本题的关键．

练习册系列答案

创新能力学习中考总复习系列答案

核按钮系列答案

高效复习新疆中考系列答案

高中总复习优化设计系列答案

六大名校中考冲刺卷系列答案

荣德基点拨中考系列答案

上海名师导学系列答案

八斗才名校直通车系列答案

中考冲刺仿真测试卷系列答案

单元评估AB卷系列答案

相关题目

已知函数f（x）=

sin2x+2cos²x+1．
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）设△ABC内角A，B，C的对边分别为a，b，c，且c=

，f（C）=3，若向量

=（sinA，-1）与向量

=（2，sinB）垂直，求a，b的值．

（2013•湛江二模）如图，已知平面上直线l₁∥l₂，A、B分别是l₁、l₂上的动点，C是l₁，l₂之间一定点，C到l₁的距离CM=1，C到l₂的距离CN=

，△ABC内角A、B、C所对边分别为a、b、c，a＞b，且bcosB=acosA
（1）判断三角形△ABC的形状；
（2）记∠ACM=θ，f（θ）=

，求f（θ）的最大值．

=(sinx，-1)，

)，函数f(x)=(

-2
（1）求函数f（x）的值域；
（2）已知a，b，c分别为△ABC内角A，B，C的对边，a=2

，且f（A）=1，求A和△ABC面积的最大值．

已知△ABC内角A、B、C的对边分别为a、b、c，且c=3，C=

=（1，sin A）与

=（2，sin B）共线．
（1）求a，b的值；
（2）求△ABC的面积和外接圆的面积．

函数f（x）=Asin（?x+φ）（其中A＞0，|φ|＜

）的图象如图所示，把函数f（x）的图象向右平移

个单位，再向下平移1个单位，得到函数y=g（x）的图象．
（1）若直线y=m与函数g（x）图象在x∈[0，

]时有两个公共点，其横坐标分别为x₁，x₂，求g（x₁+x₂）的值；
（2）已知△ABC内角A、B、C的对边分别为a、b、c，且c=3，g（C）=0．若向量

=(2，sinB)共线，求a、b的值．