题目内容
 函数f(x)=Asin(?x+φ)(其中A>0,|φ|<
函数f(x)=Asin(?x+φ)(其中A>0,|φ|<| π |
| 2 |
| π |
| 4 |
(1)若直线y=m与函数g(x)图象在x∈[0,
| π |
| 2 |
(2)已知△ABC内角A、B、C的对边分别为a、b、c,且c=3,g(C)=0.若向量
| m |
| n |
分析:(1)由函数f(x)的图象可得周期,可得ω,代点(
,0)结合φ的范围可得其值,再由图象变换可得g(x)图象,由对称性可得所求;(Ⅱ)由g(C)=0可得角C,
由向量共线可得sinB-2sinA=0.由正余弦定理可得ab的方程组,解方程组可得.
| π |
| 3 |
由向量共线可得sinB-2sinA=0.由正余弦定理可得ab的方程组,解方程组可得.
解答:解:(1)由函数f(x)的图象可得T=4(
-
)=
,解得ω=2,
又2×
+?=π,∴?=
,∴f(x)=sin(2x+
),
由图象变换,得g(x)=f(x-
)-1=sin(2x-
)-1,
由函数图象的对称性,有g(x1+x2)=g(
)=-
;
(Ⅱ)∵g(C)=sin(2C-
)-1=0,∴sin(2C-
)=1
又∵0<C<π,∴-
<2C-
<
,
∴2C-
=
,∴C=
,
∵
与
共线,∴sinB-2sinA=0.
由正弦定理得
=
,得b=2a,①
∵c=3,由余弦定理得9=a2+b2-2abcos
,②
解方程组①②可得
| 7π |
| 12 |
| π |
| 3 |
| 2π |
| ω |
又2×
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
由图象变换,得g(x)=f(x-
| π |
| 4 |
| π |
| 6 |
由函数图象的对称性,有g(x1+x2)=g(
| 2π |
| 3 |
| 3 |
| 2 |
(Ⅱ)∵g(C)=sin(2C-
| π |
| 6 |
| π |
| 6 |
又∵0<C<π,∴-
| π |
| 6 |
| π |
| 6 |
| 11π |
| 6 |
∴2C-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
∵
| m |
| n |
由正弦定理得
| a |
| sinA |
| b |
| sinB |
∵c=3,由余弦定理得9=a2+b2-2abcos
| π |
| 3 |
解方程组①②可得
|
点评:本题考查三角函数图象和性质,涉及图象的变换和正余弦定理,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
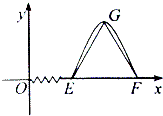 已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是边长为2的正三角形,则f(1)=( )
已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是边长为2的正三角形,则f(1)=( )A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2008)的值等于
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2008)的值等于 函数f(x)=Asin(ωx+?)(其中A>0,ω>0,
函数f(x)=Asin(ωx+?)(其中A>0,ω>0,