题目内容
数列 是一个首项为4,公比为2的等比数,Sn是{an}的前n项和.
是一个首项为4,公比为2的等比数,Sn是{an}的前n项和.(1)求数列{an}的通项及Sn
(2)设点列
 试求出一个半径最小的圆,使点列Qn中任何一个点都不在该圆外部.
试求出一个半径最小的圆,使点列Qn中任何一个点都不在该圆外部.
【答案】分析:(1)根据数列 是一个首项为4,公比为2的等比数,可得
是一个首项为4,公比为2的等比数,可得 ,从而求出{an}是以1为首项,
,从而求出{an}是以1为首项, 为公差的等差数列,即可求出数列{an}的通项及Sn;
为公差的等差数列,即可求出数列{an}的通项及Sn;
(2)设Qn(x,y),从而可得Qn在直线3x-2y-1=0上,横坐标、纵坐标随n的增大而减小,并与 无限接近,故所求圆就是以(1,1)、
无限接近,故所求圆就是以(1,1)、 为直径端点的圆.
为直径端点的圆.
解答:解:(1)∵ ∴a1=1
∴a1=1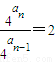 ∴
∴
即 故{an}是以1为首项,
故{an}是以1为首项, 为公差的等差数列 (3分)
为公差的等差数列 (3分)
∴ ,
, (5分)
(5分)
(2)设Qn(x,y)∴
由此可得Qn在直线3x-2y-1=0上 (8分)
横坐标、纵坐标随n的增大而减小,并与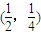 无限接近,
无限接近,
故所求圆就是以(1,1)、 为直径端点的圆即
为直径端点的圆即 (12分)
(12分)
点评:本题主要考查了数列的通项公式和数列的求和,以及极限的思想,属于中档题.
 是一个首项为4,公比为2的等比数,可得
是一个首项为4,公比为2的等比数,可得 ,从而求出{an}是以1为首项,
,从而求出{an}是以1为首项, 为公差的等差数列,即可求出数列{an}的通项及Sn;
为公差的等差数列,即可求出数列{an}的通项及Sn;(2)设Qn(x,y),从而可得Qn在直线3x-2y-1=0上,横坐标、纵坐标随n的增大而减小,并与
 无限接近,故所求圆就是以(1,1)、
无限接近,故所求圆就是以(1,1)、 为直径端点的圆.
为直径端点的圆.解答:解:(1)∵
 ∴a1=1
∴a1=1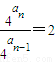 ∴
∴
即
 故{an}是以1为首项,
故{an}是以1为首项, 为公差的等差数列 (3分)
为公差的等差数列 (3分)∴
 ,
, (5分)
(5分)(2)设Qn(x,y)∴

由此可得Qn在直线3x-2y-1=0上 (8分)
横坐标、纵坐标随n的增大而减小,并与
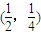 无限接近,
无限接近,故所求圆就是以(1,1)、
 为直径端点的圆即
为直径端点的圆即 (12分)
(12分)点评:本题主要考查了数列的通项公式和数列的求和,以及极限的思想,属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列
中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列 、公差为
、公差为
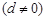 的无穷等差数列.
的无穷等差数列. ,
, 成等比数列,求其公比
成等比数列,求其公比 .
. ,从数列
,从数列 ,从数列
,从数列
 项(设
项(设 )作为一个等比数列的第1项、第2项.求证:当
)作为一个等比数列的第1项、第2项.求证:当 为大于1的正整数时,该数列为
为大于1的正整数时,该数列为 中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列
中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列 、公差为
、公差为
 的无穷等差数列.
的无穷等差数列.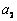 ,
, 成等比数列,求其公比
成等比数列,求其公比 .
. ,从数列
,从数列 ,从数列
,从数列
 项(设
项(设 )作为一个等比数列的第1项、第2项.求证:当
)作为一个等比数列的第1项、第2项.求证:当 为大于1的正整数时,该数列为
为大于1的正整数时,该数列为 中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列
中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列 、公差为
、公差为
 的无穷等差数列.
的无穷等差数列. ,
, 成等比数列,求其公比
成等比数列,求其公比 .
. ,从数列
,从数列 ,从数列
,从数列
 项(设
项(设 )作为一个等比数列的第1项、第2项,试问当且仅当
)作为一个等比数列的第1项、第2项,试问当且仅当 为何值时,该数列为
为何值时,该数列为