Question

设抛物线y²=4x的焦点为F，过点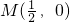的直线与抛物线相交于A，B两点，与抛物线的准线相交于点C，|BF|=2，则△BCF与△ACF的面积之比=

1. A.
   
2. B.
   
3. C.
   
4. D.
   2

Answer 1

B
分析：先求得抛物线的焦点坐标和准线方程，再利用抛物线定义，求得点B的坐标，从而写出直线AB方程，联立抛物线方程求得A点坐标，从而得到A到准线的距离，最后证明所求面积之比就是B、A到准线距离之比即可
解答：抛物线y²=4x的焦点为F（1，0），准线方程为x=-1，如图，
∵|BF|=2，∴B到准线的距离为d₁=2，即B的横坐标为1，从而点B（1，2）
∵M（，0），∴直线AB方程为y=4（x-），即y=4x-2
代入抛物线方程得4x²-5x+1=0，从而点A的坐标为A（，-1）
∴点A到准线的距离d₂=1+=
∴△BCF与△ACF的面积之比====
故选 B
点评：本题主要考查了抛物线的标准方程，抛物线的定义及其几何性质，将所求面积之比转化为B、A到准线距离之比，是解决本题的关键，属中档题