题目内容
已知(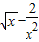 )n(n∈N*)的展开式中第五项的系数与第三项的系数的比是10:1
)n(n∈N*)的展开式中第五项的系数与第三项的系数的比是10:1(I)求展开式中各项系数的和;
(Ⅱ)求展开式中含x
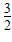 的项;
的项;(Ⅲ)求二项式系数最大项和展开式中系数最大的项.
【答案】分析:(I)由展开式中第五项的系数与第三项的系数的比是10:1,求得n=8.再令x=1得各项系数的和.
(II)在通项公式中,令x的幂指数为 ,求得r的值,即可得到展开式中含
,求得r的值,即可得到展开式中含  的项.
的项.
(III)设第r+1项的系数绝对值最大,由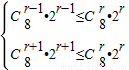 ,解得5≤r≤6,由此可得二项式系数最大项和展开式中系数最大的项.
,解得5≤r≤6,由此可得二项式系数最大项和展开式中系数最大的项.
解答:解:(I)由题可知,第5项系数为:Cn4•(-2)4,
第3项系数为Cn2•(-2)2,∴Cn4•(-2)4=10Cn2•(-2)2,∴n=8.
令x=1得各项系数的和为:(1-2)8=1.
(II)通项为:Tr+1=C8r•( )8-r•(-
)8-r•(- )r=C8r•(-2)r•
)r=C8r•(-2)r• ,
,
令 ,∴r=1,∴展开式中含
,∴r=1,∴展开式中含 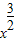 的项为T2=-16
的项为T2=-16 .
.
(III)设第r+1项的系数绝对值最大,则有 ,解得5≤r≤6,
,解得5≤r≤6,
∴系数最大的项为T7=1792•
由n=8知第5项二项式系数最大T5=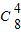 •(-2)4•x-6=1120•
•(-2)4•x-6=1120• .
.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.
(II)在通项公式中,令x的幂指数为
 ,求得r的值,即可得到展开式中含
,求得r的值,即可得到展开式中含  的项.
的项.(III)设第r+1项的系数绝对值最大,由
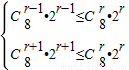 ,解得5≤r≤6,由此可得二项式系数最大项和展开式中系数最大的项.
,解得5≤r≤6,由此可得二项式系数最大项和展开式中系数最大的项.解答:解:(I)由题可知,第5项系数为:Cn4•(-2)4,
第3项系数为Cn2•(-2)2,∴Cn4•(-2)4=10Cn2•(-2)2,∴n=8.
令x=1得各项系数的和为:(1-2)8=1.
(II)通项为:Tr+1=C8r•(
 )8-r•(-
)8-r•(- )r=C8r•(-2)r•
)r=C8r•(-2)r• ,
,令
 ,∴r=1,∴展开式中含
,∴r=1,∴展开式中含 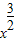 的项为T2=-16
的项为T2=-16 .
.(III)设第r+1项的系数绝对值最大,则有
 ,解得5≤r≤6,
,解得5≤r≤6,∴系数最大的项为T7=1792•

由n=8知第5项二项式系数最大T5=
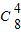 •(-2)4•x-6=1120•
•(-2)4•x-6=1120• .
.点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
相关题目
已知m、n为两条直线,α,β为两个平面,给出下列命题:( )
①
?m⊥n②
?m∥n③
?m∥n④
?α⊥β.
①
|
|
|
|
| A、②③ | B、①③④ |
| C、①②③ | D、①②③④ |