题目内容
若数列{an}的前n项和Sn＝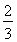
an＋
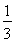，则{an}的通项公式是an＝________.
(－2)n－1
【解析】当n＝1时，S1＝
a1＋
，∴a1＝1.
当n≥2时，an＝Sn－Sn－1＝
an＋
－
＝
(an－an－1)，
∴an＝－2an－1，即
＝－2，
∴{an}是以1为首项的等比数列，其公比为－2，
∴an＝1×(－2)n－1，即an＝(－2)n－1.
练习册系列答案
相关题目
题目内容
若数列{an}的前n项和S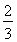n＝an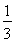＋，则{an}的通项公式是an＝________.
(－2)n－1
【解析】当n＝1时，S1＝a1＋，∴a1＝1.
当n≥2时，an＝Sn－Sn－1＝an＋－＝ (an－an－1)，
∴an＝－2an－1，即＝－2，
∴{an}是以1为首项的等比数列，其公比为－2，
∴an＝1×(－2)n－1，即an＝(－2)n－1.
