题目内容
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)试求函数![]() 零点的个数,并证明你的结论.
零点的个数,并证明你的结论.
【答案】(1)见解析(2)见解析
【解析】
(1)求导得![]() ,分类讨论当
,分类讨论当![]() 和
和![]() 时,利用导函数研究函数
时,利用导函数研究函数![]() 的单调性;
的单调性;
(2)根据题意,当![]() 时,
时,![]() ,函数
,函数![]() 有且只有一个零点
有且只有一个零点![]() ;当
;当![]() 时,利用零点存在性定理,得出
时,利用零点存在性定理,得出![]() 在
在![]() 上有且只有一个零点;当
上有且只有一个零点;当![]() 时,根据零点存在性定理和单调性讨论零点个数,综合即可得出结论.
时,根据零点存在性定理和单调性讨论零点个数,综合即可得出结论.
解:(1)![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,由
时,由![]() ,
,
得![]() ,
,
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 上单调递减,
上单调递减,
(2)![]() 时,
时,![]() ,函数
,函数![]() 有且只有一个零点
有且只有一个零点![]() ,
,
当![]() 时,因为
时,因为![]() ,
,![]() ,
,
由根的存在定理可知,在![]() 上存在零点,
上存在零点,
又因为![]() 在
在![]() 上单调递增,
上单调递增,
从而![]() 在
在![]() 上有且只有一个零点.
上有且只有一个零点.
当![]() 时,由(1)可知
时,由(1)可知![]() 存在最大值,
存在最大值,
且![]() ,
,
①若![]() ,即
,即![]() 时,函数
时,函数![]() 无零点,
无零点,
②若![]() ,即
,即![]() 时,函数
时,函数![]() 有且只有一个零点
有且只有一个零点![]() ,
,
③若![]() ,即
,即![]() 时,
时,
因为![]() ,
,
所以![]() 在
在![]() 上存在零点,
上存在零点,
由(1)可知![]() 在
在![]() 单调递增,
单调递增,
所以![]() 在
在![]() 上有且只有一个零,
上有且只有一个零,
下面寻找![]() ,使得满足
,使得满足![]() ,且
,且![]() ,
,
先证明若![]() ,则
,则![]() ,
,
令![]() ,
,![]() ,
,
所以函数![]() 在
在![]() 单调递增,
单调递增,
所以![]() ,
,
所以![]() ,
,
所以当![]() 时,
时,
![]() ,
,
令![]() ,解得
,解得![]() ,
,
取![]() ,
,
则![]() ,
,
又因为![]() ,
,
所以![]() 在
在![]() 存在零点,
存在零点,
由(1)可知![]() 在
在![]() 有且只有一个零点,
有且只有一个零点,
所以![]() 有且只有两零点,
有且只有两零点,
综上,当![]() 或
或![]() 时函数
时函数![]() 有且只有一个零点,
有且只有一个零点,
当![]() 时,函数
时,函数![]() 有且只有两个零点,
有且只有两个零点,
当![]() 时,函数
时,函数![]() 无零点.
无零点.

 阅读快车系列答案
阅读快车系列答案【题目】已知函数![]() ,
,![]()
![]() .
.
(1)当x≥0时,f(x)≤h(x)恒成立,求a的取值范围;
(2)当x<0时,研究函数F(x)=h(x)﹣g(x)的零点个数;
(3)求证:![]() (参考数据:ln1.1≈0.0953).
(参考数据:ln1.1≈0.0953).
【题目】已知椭圆![]() :
:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() 和
和![]() ,右顶点为
,右顶点为![]() ,且
,且![]() ,短轴长为
,短轴长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过点![]() 作垂直
作垂直![]() 轴的直线
轴的直线![]() ,点
,点![]() 为直线
为直线![]() 上纵坐标不为零的任意一点,过
上纵坐标不为零的任意一点,过![]() 作
作![]() 的垂线交椭圆
的垂线交椭圆![]() 于点
于点![]() 和
和![]() ,当
,当![]() 时,求此时四边形
时,求此时四边形![]() 的面积.
的面积.
【题目】京广高速铁路(又称京广高铁)是中国运营中的高速客运专线之一,被誉为世界上运营里程最长的高速铁路,在出行人群中越来越受欢迎.现交通部门利用大数据工具随机抽取了沿线城市出行人群中的![]() 名旅客进行调查统计,得知在这
名旅客进行调查统计,得知在这![]() 名旅客中
名旅客中![]() 岁(含)以下采用乘坐京广高铁出行的占
岁(含)以下采用乘坐京广高铁出行的占![]() .
.
|
| 合计 | |
乘京广高跌 |
| ||
不乘京广高跌 | |||
合计 |
|
|
(1)请完成的![]() 列联表,并由列联表中所得数据判断有多大把握认为“乘坐京广高铁出行与年龄有关”?
列联表,并由列联表中所得数据判断有多大把握认为“乘坐京广高铁出行与年龄有关”?
(2)为优化服务质量,铁路部门从这![]() 名旅客按年龄采用分层抽样的方法随机抽取
名旅客按年龄采用分层抽样的方法随机抽取![]() 人免费到广州参加座谈会,会后再进行抽奖活动,奖品共三份.由于年龄差异,规定
人免费到广州参加座谈会,会后再进行抽奖活动,奖品共三份.由于年龄差异,规定![]() 岁(含)以下的旅客若中奖每人得
岁(含)以下的旅客若中奖每人得![]() 元,
元,![]() 岁以上的旅客若中奖每人得
岁以上的旅客若中奖每人得![]() 元,这两个年龄段的得奖人数分别记为
元,这两个年龄段的得奖人数分别记为![]() 与
与![]() .设旅客抽奖所得的总金额为
.设旅客抽奖所得的总金额为![]() 元,求
元,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
参考公式: 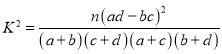 ,
,![]() 参考数据如表
参考数据如表
|
|
|
|
|
|
|
|
|
|