题目内容

解:(1)∵m·n=1,
即![]() sin
sin ![]() cos
cos ![]() +cos2
+cos2![]() =1,
=1,
即![]() sin
sin ![]() +
+![]() c
c![]() os
os ![]() +
+![]() =1,
=1,
∴sin(![]() +
+![]() )=
)=![]() .
.
∴cos(![]() -x)=cos(x-
-x)=cos(x-![]() )
)
=-cos(x+![]() )=-[1-2sin2(
)=-[1-2sin2(![]() +
+![]() )]
)]
=2·(![]() )2-1=-
)2-1=-![]() .
.
(2)∵(2a-c)cos B=bcos C,
由正弦定理得(2sin ![]() A-sin C)cos B=sin Bcos C.
A-sin C)cos B=sin Bcos C.
∴2sin Acos B-cos Bsin C=sin Bcos C,
∴2sin Acos B=sin(B+C),
∵A+B+C=π,∴si![]() n(B+C)=sin A,且sin A
n(B+C)=sin A,且sin A![]() ≠0,
≠0,
∴cos B=![]() ,B=
,B=![]() ,∴
,∴![]() 0<A
0<A![]() <
<![]() .
.
∴![]() <
<![]() +
+![]() <
<![]() ,
,![]() <sin(
<sin(![]() +
+![]() )<1.
)<1.
又∵f(x)=m·n=sin(![]() +
+![]() )+
)+![]() ,
,
∴f(A)=sin(![]() +
+![]() )+
)+![]() ,
,
故函数f(A)的取值范围是(1,![]() ).
).

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
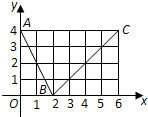 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=