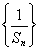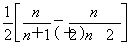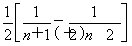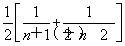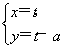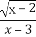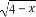题目内容
已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x.
(1)解关于x的不等式g(x)≥f(x)-|x-1|;
(2)如果对?x∈R,不等式g(x)+c≤f(x)-|x-1|恒成立,求实数c的取值范围.
(1) (2)
(2)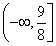
【解析】(1)∵函数f(x)和g(x)的图象关于原点对称,
∴g(x)=-f(-x)=-(x2-2x),
∴g(x)=-x2+2x,x∈R.
∴原不等式可化为2x2-|x-1|≤0.
上面的不等式等价于 ①或
①或 ②
②
由①得-1≤x≤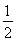 ,而②无解.
,而②无解.
∴原不等式的解集为 .
.
(2)不等式g(x)+c≤f(x)-|x-1|可化为c≤2x2-|x-1|.
令函数F(x)=
当x≥1时,F(x)min=2;
当x<1时,F(x)min=F =-
=- .
.
综上,可得函数F(x)的最小值为-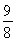 ,
,
所以实数c的取值范围是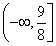 .
.

练习册系列答案
相关题目