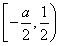题目内容
设函数f(x)＝|x－1|＋|x－2|.
(1)画出函数y＝f(x)的图象；
(2)若不等式|a＋b|＋|a－b|≥|a|f(x)( a≠0，a，b∈R)恒成立，求实数x的取值范围．
（1）
（2）
≤x≤
【解析】(1)f(x)＝
图象如图．
(2)由|a＋b|＋|a－b|≥|a|f(x)得
≥f(x)．
又因为
≥
＝2.
则有2≥f(x)．解不等式2≥|x－1|＋|x－2|得≤x≤.
即x的取值范围为≤x≤
练习册系列答案
世纪百通期末金卷系列答案
相关题目
