题目内容
2.判断下列各式的符号:(1)sinθ•cosθ($\frac{π}{2}$<θ<π);
(2)$\frac{sinθ}{cosθ}$(2π<θ<$\frac{5π}{2}$).
分析 根据θ的范围判断θ的象限,判断sinθ,cosθ的符号,从而得出代数式的符号.
解答 解:(1)∵$\frac{π}{2}$<θ<π,
∴sinθ>0,cosθ<0.
∴sinθ•cosθ<0.
(2)∵2π<θ<$\frac{5π}{2}$,
∴sinθ>0,cosθ>0.
∴$\frac{sinθ}{cosθ}$>0.
点评 本题考查了象限角的三角函数符号,根据三角函数的定义和象限记忆三角函数符号,属于基础题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
12.若不等式组$\left\{\begin{array}{l}x-y+2≥0\\ y≥m\\ 0≤x≤2\end{array}\right.$表示的平面区域是一个三角形,则m的取值范围是( )
| A. | [2,4) | B. | [2,+∞) | C. | [2,4] | D. | (2,4] |
10.已知等差数列{an}的前n项和为Sn,满足S5=S9,且a1>0.则Sn中最大的是( )
| A. | S6 | B. | S7 | C. | S8 | D. | S15 |
7.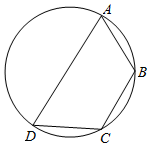 如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )
如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )
 如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )
如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )| A. | $\sqrt{3}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | $\sqrt{3}$+1 | D. | $\frac{\sqrt{3}}{2}$+$\frac{1}{2}$ |