Question

【题目】如图，椭圆的右顶点为，左、右焦点分别为，过点且斜率为的直线与轴交于点，与椭圆交于另一个点，且点在轴上的射影恰好为点．

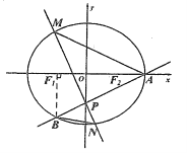
(1)求椭圆的标准方程；

(2)过点的直线与椭圆交于两点（不与重合），若，求直线的方程.

Answer 1

【答案】(1) ；(2) 或．

【解析】试题分析：（Ⅰ）当时，BF1⊥x轴，求出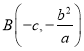，列出方程组，求出a，b即可得到椭圆的标准方程．

（Ⅱ）通过民间的比推出．设M（x1，y1），N（x2，y2），设MN方程为y=kx﹣1，联立直线与椭圆方程，利用韦达定理转化情况直线的斜率，求出直线方程．

试题解析：

（1）当时， 轴，得到点，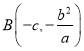

所以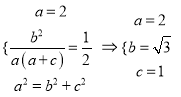，所以椭圆的方程是．

（2）因为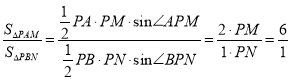， 所以．

设，则，有

①当斜率不存在， 的方程为，

或，(不合条件,舍去)

②当斜率存在，由（Ⅰ）可知，设方程为，

联立方程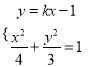得： ．

由韦达定理可得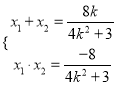，将代入可得，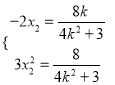

即．所以．

所以直线的方程为或．